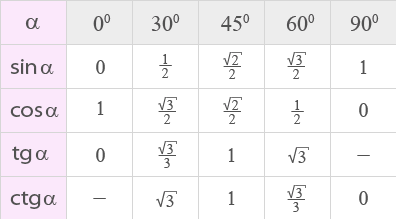
Таблица основных тригонометрических функций для углов 0, 30, 45, 60, 90 градусов

Для начала определим понятие «тригонометрические функции».

Из учебника геометрии нам известно, что к тригонометрическим функциям относятся синус (sin), косинус (cos), тангенс(tg), котангенс(ctg), секанс (sec) и косеканс (cosec). В данной статье мы разберем первые четыре.
Следуя тригонометрическим определениям функций sin, cos, tg и ctg можно найти их значения для углов 0 и 90 градусов:
sin 0⁰= 0, cos 0⁰=1, tg 0⁰=0, ctg 0⁰ — не определяется;

sin 90⁰=1, cos 90⁰=0, ctg 90⁰=0, tg 90° — не определяется.

На уроках геометрии изучая прямоугольные треугольники в основном вычисляют тригонометрические функции углов 0°, 30°, 45°, 60° и 90°.

Извлеченные значения тригонометрических функций для углов были составлены в таблицу, которую называют таблица тригонометрических функций, таблица значений тригонометрических функций, таблицей тригонометрических функций углов и т.д

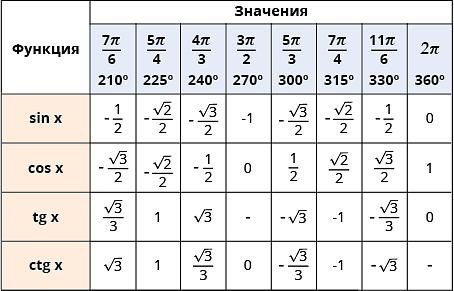
Используя формулы приведения, тригонометрическая таблица может быть увеличена до угла 360° и  2π радиан:

Используя особенности цикличности тригонометрических функций, любой угол, отличный от уже известного на 360°, может быть посчитан и занесен в таблицу. Например, тригонометрическая функция для угла 30° будет иметь такое же значение и для угла 30°+360°, и для угла 30°+2⋅360°, и для угла 30°+3⋅360° и т.д.

При помощи таблицы значений углов тригонометрических функций можно найти величину всех углов единичной окружности.

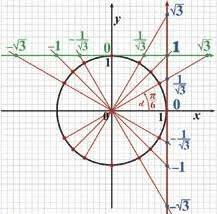
Как пользоваться таблицей тригонометрических функций

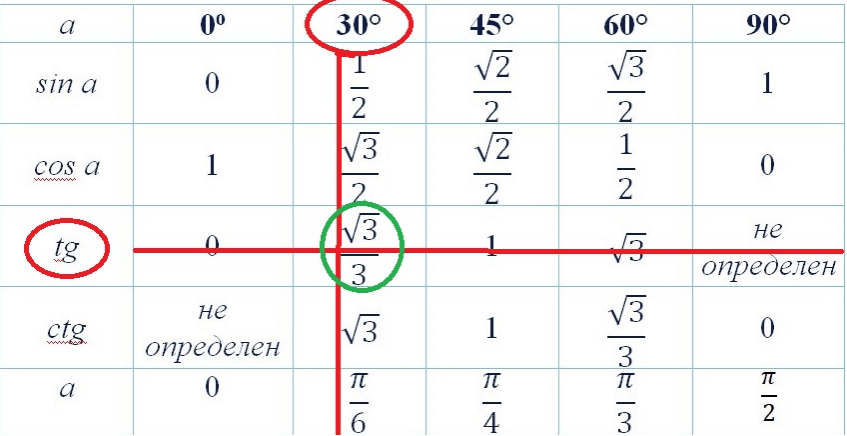
Для того чтобы посчитать тригонометрическую функцию, достаточно отыскать нужную тригонометрическую функцию и значение угла или радиан в таблице. Там где пересекаются строка с функцией и столбец со значением, будет необходимое  значение тригонометрической функции.

На изображении, представленном ниже,  можно проследить, каким образом определить значение тангенса  30⁰, которое равно: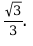

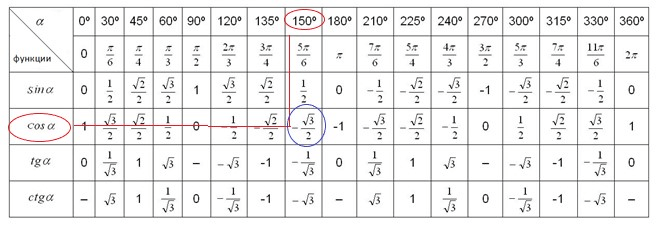
Точно также используется расширенная тригонометрическая таблица. Главным достоинством  ее использования является подсчет тригонометрической функции практически любого угла. Например, с легкостью мы можем найти значение

cos 1230° = cos (1230°−360°) = cos (870°−360°) = cos (510°−360°) = cos 150°:

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Таблица тригонометрических функций Брадиса

Если вам необходимо найти значение какого-то угла для его целого значения, целых градусов и целых минут, то можно воспользоваться таблицами Брадиса. Существует 2 вида таблицы: таблица для sin и cos и таблица для tg и ctg.

Таблицы Брадиса помогают найти максимально приближенное значение тригонометрических функций. 

Как использовать таблицы Брадиса

Попробуем на практике как работать с таблицами Брадиса. 

Пользуясь таблицей Брадиса для синусов, вычислим sin 24°36′. Для этого в столбце слева таблицы синусов и косинусов выбираем значение градусов – 24°, а в верхней строке обнаруживаем значение минут – 36′. На их пересечении получаем необходимое значение:

sin 24°36′. = 0,4163.

Для того чтобы найти значения sin 24°37′ необходимо обратиться к поправке в правой части таблицы. В нашем примере к значению 36′, которое есть в таблице, нужно прибавить поправку для 1′ , которая равна 0,0003. Получаем: sin⁡24°37′=0,4163+0,0003=0,4166.

Чтобы посчитать значение sin⁡24°40′  также воспользуемся поправкой в правой части таблицы. В этом случае от значения 42′, которое есть в таблице, отнимаем поправку для 2′, которая равна 0,0005. Получим: sin⁡24°40′ = 0,4179 — 0,0005 = 0,4174.

Чтобы расчищать косинус, выполняем те же манипуляции, но градусы смотрим в правом столбце, а минуты – в нижней колонке таблицы. Например, cos 15°=0,9655. Для значений тангенса до 90° и котангенса малого угла поправок нет.

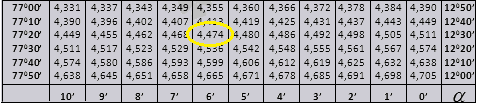
Для закрепления полученных знаний найдем tg 76°34′. Согласно таблице он 4,187.

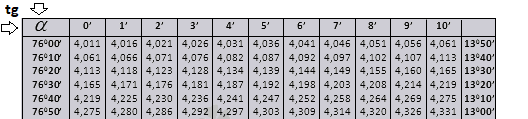
Найдем ctg 12°36′=4,474.