Координатная прямая (числовая прямая), координатный луч
Введение в координатную геометрию
Система геометрии, в которой положение точек на плоскости описывается упорядоченной парой чисел.
Плоскость — это поверхность, бесконечно простирающаяся в обоих направлениях. Если бы мы поместили точку на плоскости, координатная геометрия дала бы нам способ точно описать, где она находится, с помощью двух чисел.
Что такое координаты?
Чтобы показать концепцию, изучим сетку выше. Столбцы помечены A, B, C и т. д. Строки сгруппированы 1, 2, 3 и т.д. сверху. Мы видим, что X располагается в ячейке D3; то есть столбик D, строчка 3.
D и 3 именуются координатами. Она состоит из двух частей: строчки и столбика. В каждой строке много полей, и в каждом столбце много полей. Номы можем найти одно безальтернативное поле, где пересекаются столбец и строка.
Координатная плоскость
В координатной геометрии точки располагаются на «координатной плоскости», как продемонстрировано ниже. Он имеет две шкалы, одна проходит вдоль плоскости, именуемой «осью x», а другая перпендикулярна ей, называемой «осью y». (Их можно изучать как подобные столбцу и строке в абзаце выше.) Точка, в которой оси пересекаются, зовётся началом координат, где x и y равны нулю.
Определение прямой в координатной геометрии
Прямая — геометрический объект, который является прямым, бесконечно длинным и бесконечно тонким. Его местоположение определяется двумя или более точками на прямой, координаты которых известны.
Прямая проходит через обе и бесконечно продолжается в обоих направлениях.
Это то же самое, что и определение прямой в обычной планиметрии, с той лишь разницей, что мы знаем координаты задействованных точек.
Определение луча в координатной геометрии
Луч — это прямая,начинающаяся в точке с заданными координатами и бесконечно уходящая в каком-то направлении. При этом он может проходить через другую точку. Это то же самое, что и определение луча в обычной плоской геометрии, с той лишь разницей, что мы знаем координаты.
Координаты
Каждой точке пространства можно присвоить три числа относительно начальной точки. Эти три числа позволяют нам отличить любую точку от любой другой в пространстве. К счастью для вас, мы имеем дело не с тремя измерениями, а только с двумя.
Упорядоченные пары: каждая точка на координатной плоскости называется парой чисел, порядок которых важен; эти числа записываются в круглых скобках и разделяются запятой.
Координата x: число слева от запятой в упорядоченной паре является координатой x и указывает величину перемещения по оси x от начала координат. Движение происходит вправо, если число положительное, и влево, если число отрицательное.
y- координата: число справа от запятой в упорядоченной паре является y — координатой и указывает количество движения перпендикулярно оси x. Движение выше оси x, если число положительное, и ниже оси x, если число отрицательное.
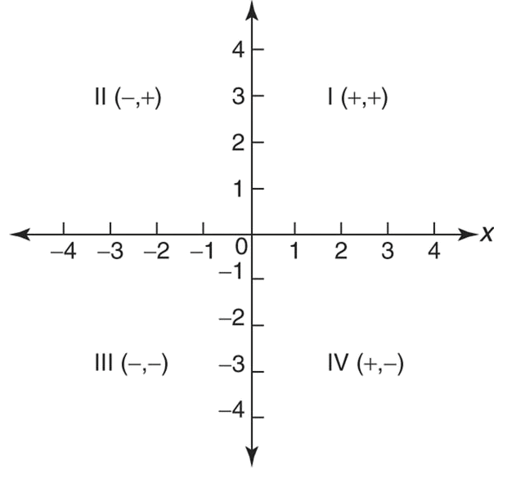
- В квадранте I x всегда положителен, а y всегда положителен.
- В квадранте II x всегда отрицателен, а y всегда положителен.
- В квадранте III x всегда отрицателен, а y всегда отрицателен.
- В квадранте IV x всегда положителен, а y всегда отрицателен.
Точка, связанная с упорядоченной парой действительных чисел, называется графом упорядоченной пары.
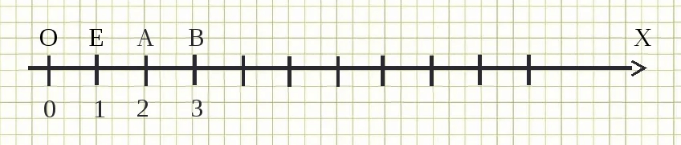
Определите A, B, C, D, E и F на графике координат на рисунке.
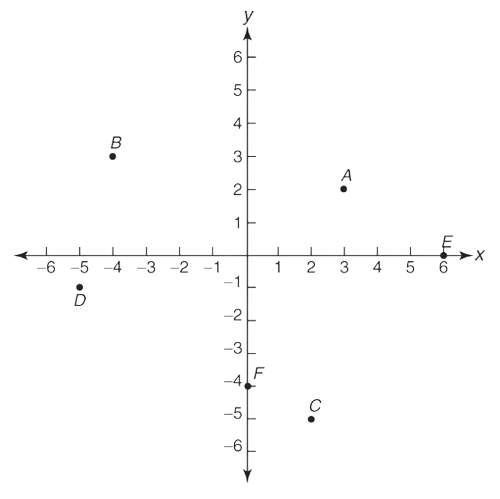
Нахождение координат конкретных точек на плоскости.
A (3;2), В (-4;3), C (2; -5), D (-1; -5), Е (6,0) и F (-4;0)
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Расстояние между двумя точками
Учитывая координаты двух точек, расстояние D определяется как:
\[D=\sqrt{d x^{2}+d y^{2}}\]
Где:
dx — разница между x-координатами точек
dy — разница между y-координатами точек
Соответствие между точками и действительными числами
Прямая может содержать много точек. Они непосредственно связаны с действительными числами. Это можно обозначить как взаимно очевидное соответствие.
Любая точка на прямой координат соответствует одному действительному числу, а каждое любое число соответствует одной точке на прямой.
Чтобы лучше уяснить это правило, нужно обозначить точку на прямой координат и посмотреть, какому числу соответствует знак. Если эта точка соотносится с началом координат, она будет помечена нулем. Если не совпадает с началом, откладываем нужное число единичных отрезков до достижения заданного знака. Этой точке будет соответствовать число. В изложенном ниже примере воочию продемонстрируем этот постулат.
Если мы не можем отыскать точку, откладывая единичные отрезки, нам также нужно обозначить точки, составляющие десятую, сотую или тысячную часть его. Подробно это правило можно увидеть на образце.
Отложив несколько таких промежутков, мы можем получить не только целое число, но и дробное — как отрицательное, так и положительное. Помеченные промежутки помогут нам найти необходимую точку на прямой координат. Это могут быть как целые числа, так и дробные. Впрочем, на прямой есть точки, которые чрезвычайно сложно найти с помощью отдельных отрезков. Они соответствуют десятичным дробям. Чтобы найти аналогичную точку, нужно отложить один отрезок, десятую, сотую, тысячную, десятитысячную и другие части.
Множество действительных чисел включает в себя все, которые возможно записать в виде дроби.
Каждой точке на прямой координат соответствует конкретное действительное число.
Различные точки обозначают разные числа.
Если число не является целым, мы должны обозначить несколько отрезков (единичных), а также десятые, сотые доли в заданном направлении. К примеру, 400350 соответствует точке на прямой координат, в которую возможно попасть из начала координат, отложив в положительном направлении 400 единичных отрезков, 3 десятичных, и 5 тысячных.
Каждая точка на прямой соответствует действительному числу, которое помечается на координатной прямой. Из-за данного суждения прямая иногда определяется как числовая прямая.
Выполнение любых работ по математике
Популярные статьи
Примеры решения матриц с ответами
Общее уравнение плоскости
Метод Крамера – теорема, примеры решений
Нахождение площади фигуры ограниченной линиями y=f(x), x=g(y)