Нахождение координат вектора через координаты точек
Вектор – это направленный отрезок, т.е. отрезок, имеющий длину и определенное направление. Графически вектор изображается в виде направленных отрезков определенной длины.
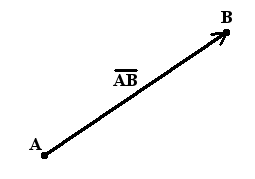
Вектор, имеющий начальную точку А и конечную точку В, обозначается \[\overrightarrow{A B}\](рис. 1).
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора \[\overrightarrow{A B}\]. Длина вектора \[\overrightarrow{A B}\] обозначается как: \[|\overrightarrow{A B}|\]
Векторы параллельные одной прямой или лежащие на одной прямой, называются коллинеарными векторами.
Единичный вектор или орт — это вектор, длина которого равна единице.
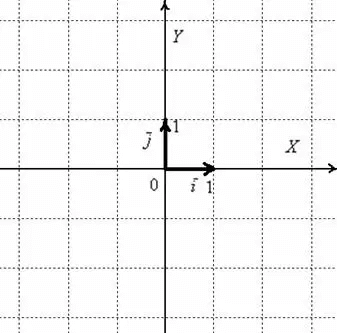
Правило нахождения координат вектора
Отложим от начала системы координат два единичных вектора, то есть векторы, длины которых равны единице. Направление вектора \[\bar{i}\] должно совпадать с осью \[O x\], а направление вектора \[\bar{j}\] с осью \[O y\].
Векторы \[\bar{i}, \bar{j}\] — рассматриваемые векторы называются векторами координат или ортами. Эти векторы образуют базис поверхности. Иногда построенный базис называют ортонормированным базисом плоскости.
Обозначение: базис обычно пишется в круглых скобках, внутри которых в строгом порядке перечисляются векторы.
Любой вектор плоскости выражается по формуле нахождения координат вектора:
Где числа в этом базисе называются векторными координатами. Но само выражение называется векторным разложением.
Как выразить вектор через его координаты
Чтобы выразить вектор \[\overrightarrow{A B}(a, b)\], где \[A\left(x_{1} ; y_{1}\right)\], а \[B\left(x_{2} ; y_{2}\right)\], сначала вычислим разницу между абсциссами \[x\], чтобы получить \[a\], затем вычислим разницу между ординатами \[y\], чтобы получить \[b\]:
Пример 1
Найти координаты \[\overrightarrow{A B}\] при значении координат точек \[A(3 ; 2), B(6 ; 9)\].
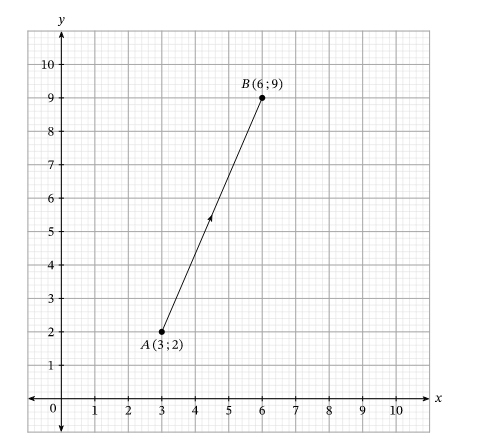
Решение:
Горизонтальное расстояние равно разнице между абсциссами \[x\], т.е. 6−3=3. Вертикальное расстояние равно разнице между ординатами \[y\], где 9−2=7.
Поэтому мы можем обозначить вектор от А до В как:
Нахождение координат вектора в пространстве
Теперь рассмотрим векторы в трехмерном пространстве, здесь все почти так же, как на плоскости, но будет добавлена только одна дополнительная координата.
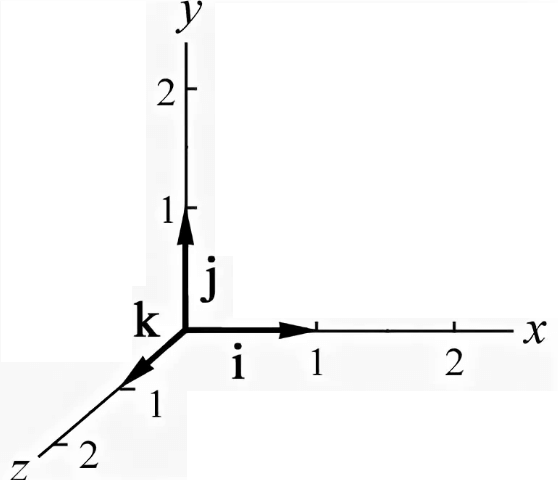
Любой вектор в пространстве выражается следующим образом:
\[\vec{v}=v_{1} \cdot \vec{i}+v_{2} \cdot \vec{j}+v_{3} \cdot \vec{k}\], где координаты вектора (числа) в заданном базисе.
Пример 2
Нужно найти вектор, соединяющий точку А (начало) с координатами (4, 5, 6) с точкой В (конец) с координатами (10, 11, 12).
Решение:
Вектор направлен из точки А в точку В и может быть обозначен как \[\overrightarrow{A B}\]. Таким образом:

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Как записать вектор на основе единичных векторов
Если мы перейдем от начальной точки к конечной точке \[C\left(x_{y} ; y_{1}\right) D\left(x_{2} ; y_{2}\right)\], это описывает вектор, который представляет собой смещение на расстояние в направлении \[\overrightarrow{C D}\left(x_{2}-x_{1}\right) x\] затем с расстояния в направлении \[\left(y_{2}-y_{1}\right) y\].
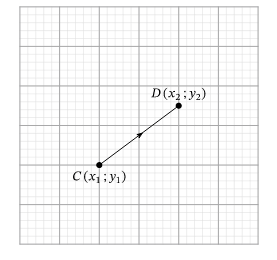
Мы можем обозначить этот вектор двумя способами:
\[\overrightarrow{C D}=\left(x_{2}-x_{1}, y_{2}-y_{1}\right)\] или \[\overrightarrow{C D}=\left(x_{2}-x_{1}\right) i+\left(y_{2}-y_{1}\right) \vec{j}\]
Пример 3
Выразить вектор в виде суммы единичных векторов.
Зная, что каждый квадрат сетки имеет длину 1, представим вектор \[\overrightarrow{A B}\] как \[a \vec{i}+b \vec{j}\].
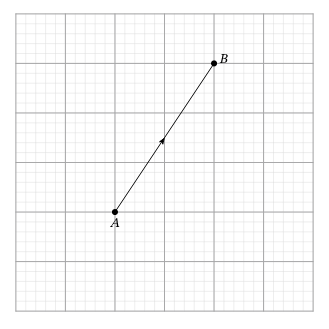
Решение:
Из точки \[A\](начало), мы перемещаем единицы в горизонтальном направлении (которое представляет собой вектор), затем мы перемещаем единицы в вертикальном направлении (что представляет собой вектор), чтобы перейти к точке \[B+2(2 \vec{i}) u+3(3 \vec{j})\].
Вектор \[\overrightarrow{A B}\] что представляет собой прямое движение от \[A\] к \[B\] , тогда равна сумме этих единичных векторов.
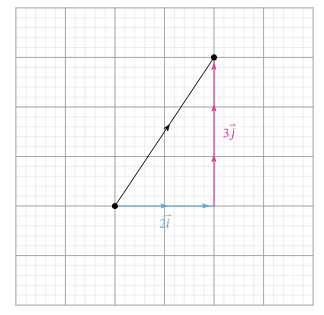
Как результат: \[\overrightarrow{A B}=2 \vec{i}+3 \vec{j}=(2,3)\].
Использование векторов и позволяет описать вектор в соответствии с количеством шагов по горизонтали и вертикали длиной 1, которые необходимо сделать, чтобы пройти от начала до конца. Обратите внимание, что отрицательные коэффициенты представляют движение влево или вниз соответственно.
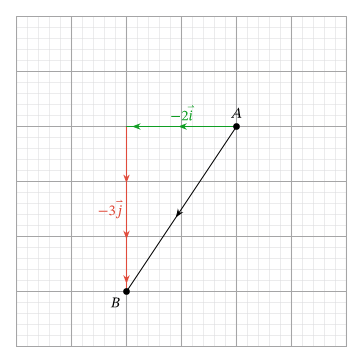
Например, приведенный выше вектор, представляющий смещение на -2 единицы в направлении и на -3 единицы в направлении \[\overrightarrow{A B}=(-2 ;-3) x y\] или \[(-2 \vec{i})+(-3 \vec{j})\].
Следует понимать разницу между координатами точки и векторными координатами:
Координаты точки — это обычные координаты в прямоугольной системе координат. Каждая точка имеет строгое место на карте, и их нельзя никуда перемещать.
Координаты вектора — это его разложение относительно основания.
Любой вектор свободен, поэтому при желании или необходимости мы легко можем отложить его от другой точки плоскости. Записи координат точек и векторных координат выглядят одинаков, а значение координат совсем разные.
Координаты равных векторов соответственно равны.
Если точка начала вектора не совпадает с началом системы координат, тогда рассмотрим задачу. На оси \[O_{x y}\] заданы координаты точек вектора, где \[A\left(x_{a} ; y_{a}\right)\] и \[B\left(x_{b} y_{b}\right)\]. Найти координаты \[\overrightarrow{A B}\].
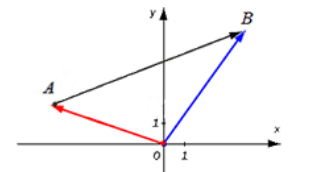
Зная формулу сложения векторов, имеем \[\overrightarrow{O A}+\overrightarrow{A B}=\overrightarrow{O B}\], следует: \[\overrightarrow{A B}=\overrightarrow{O B}-\overrightarrow{O A}\].
\[\overrightarrow{O A}\] и \[\overrightarrow{O B}\] радиус-векторы точек А и В, следовательно, координаты точек: \[\overrightarrow{O A}=\left(x_{a}, y_{a}\right), \overrightarrow{O B}=\left(x_{b} ; y_{b}\right)\].















