Расстояние от точки до плоскости: определение и примеры нахождения
В статье мы расскажем о нескольких способах того, как найти расстояние от точки до плоскости, а для лучшего понимания рассмотрим пример на эту тему.
Определение расстояние от точки до плоскости
Пусть дана плоскость χ, а в пространстве задана точка M1. Через неё проходит прямая, перпендикулярная нашей χ. H1 обозначим общую точку их пересечения. Отрезок M1H1 является перпендикуляром из M1 к \[χ\]. В обсуждаемом случае H1 есть основание перпендикуляра.
Под расстоянием от точки до плоскости понимают расстояние между этой точкой и основанием перпендикуляра, проходящего через неё к указанной плоскости.
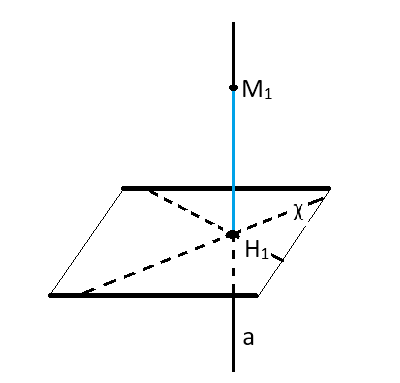
Под расстоянием от точки \[M_{1}\] до плоскости χ понимают длину перпендикуляра, проведённого из \[M_{1}\] к χ. Оно является наименьшим от M1 до любой из точек плоскости.
Докажем это:
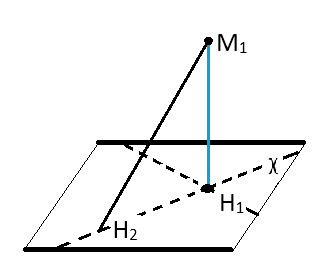
Если H2 на χ не совпадает с H1, то мы имеем прямоугольный треугольник M2H1H2. При этом M2H1 есть его катет, а M2H2 гипотенуза. Длина гипотенузы треугольника всегда больше, чем длина катета. Доказательство завершено.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Способы найти расстояние от точки до плоскости
Мы имеем точку M1 в трёхмерном пространстве с декартовыми координатами x1, y1, z1 и плоскость \[χ\]. Покажем, как в этом случае найти расстояние от M1 до \[χ\].
- Первый способ.
Он основан на использовании координат точки H1, которая является основанием перпендикуляра, проведённого из M1 к \[χ\]. После этого вычисление искомой величины происходит достаточно просто. - Второй способ.
Сначала составляем уравнение прямой, которая перпендикулярна χ и проходит через M1. Затем выясняем координаты (x2, y2, z2) пересечения прямой \[a\] и \[χ\]. Вычисляем расстояние от точки M1 до плоскости χ, формула, по которой это делается, следующая:
- Третий способ.
В прямоугольной декартовой системе координат у нас имеется плоскость χ. Её нормальное уравнение можно записать в виде:
cosα * x + cosβ * y + cosγ * z – p = 0
M1H1 вычисляется с помощью формулы:
M1H1 = cosα * x + cosβ * y + cosγ * z – p
Это следует из теоремы, гласящей, что если в трёхмерном пространстве имеется точка M1(x1,y1,z1) и имеется нормальное уравнение плоскости, которое можно записать в виде cosα * x + cosβ * y + cosγ * z – p = 0, то расстояние от точки до плоскости будет равно
M1H1 = cosα * x + cosβ * y + cosγ * z – p
потому что x=x1, y=y1, z=z1.
Требуется найти расстояние точки \[M_{1}\](-3, √2, -7) до лежащих около неё плоскостей:
- 0xy
- 2y-5=0
Решение:
- Т. к. данная координатная плоскость соответствует уравнению вида x=0, для 0yz оно нормальное. Поэтому в левую часть выражения следует подставить значения -3. Затем берём модуль значения расстояния от точки с указанными координатами. Получаем число 3.
- Делим 2y-5=0 на 2. Это позволяет нам привести его к виду y-(5/2) = 0. После соответствующих подстановок и вычисления получаем искомую величину. Она равна (5/2) — √2.
Выполнение любых работ по математике
Популярные статьи
Примеры решения матриц с ответами
Общее уравнение плоскости
Метод Крамера – теорема, примеры решений
Нахождение площади фигуры ограниченной линиями y=f(x), x=g(y)