Расстояние от точки до точки: формулы, примеры, решения
На первый взгляд может показаться, что математика сложна и коварна, но это далеко не так. Если приложить усилия к её изучению, то можно удивиться тому, насколько быстро вы измените своё мнение о ней. Давайте же разберём одну из тем, которая поможет находить расстояние от точки до точки при различных условиях. После того как вы изучите данную статью, вы можете решить предоставленные задания, чтобы лучше закрепить пройденный материал.
Математические термины
Для начала введём некоторые определения.
Расстояние между точками – это измерение отрезка, находящегося между этими точками, составляющего длину расстояния.
Эти отрезки располагаются в определенном масштабе, потому как необходимо знать единицу длины для их измерения, без этого нельзя.
Функция – это связь величин, выражаемая в зависимости одной переменной Y, от второй переменной X.
Произвольная функция (точка) – это такая точка, которую можно расположить в любом месте.
Координатная прямая – это прямая, на которой изображают точку отсчёта 0 и единичные отрезки. Прямой также задают направление.
Действительные числа – это совокупность рациональных и иррациональных чисел.
Рациональное число – это такое число, которое может находиться в виде обыкновенной дроби, в отличие от иррационального числа.
Иррациональное число – это бесконечная непериодическая десятичная дробь. Такое число нельзя представить в виде обыкновенной дроби.
Модуль или же абсолютная величина – это обязательно неотрицательное число, которое является расстоянием определённых точек.
Как определить расстояние между точками, находящимися на координатной прямой
Чтобы найти расстояние от одной точки до другой, т.е. длину этого отрезка, нужно сравнить его с другим таким отрезком в заданном масштабе.
Действительные числа
Рассмотрим этот способ на примере:
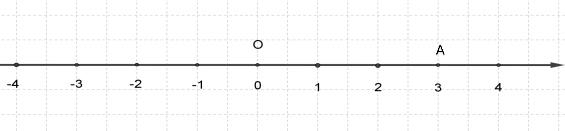
Здесь мы имеем координатную прямую OX, на которой отмечена точка A. Она произвольная, поэтому мы можем задать ей любое действительное число, пусть это будет 3.
Отрезок – это единица длины, поэтому все отрезки, что мы отложили от точки O нужно сложить, вследствие чего полученное количество единичных отрезков будет равняться длине отрезка OA. В данном случае здесь три отрезка, поэтому и ответ таков.
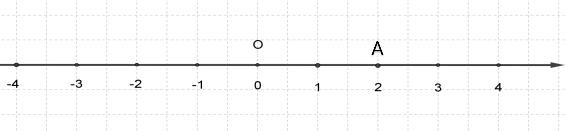
Ещё один пример, где точку отсчёта O и произвольную точку A соединяют 2 отрезка. Это значит, что расстояние длин всех единичных отрезков OA равно 2. Если же точка A будет иметь другое число, например: 6, то мы откладываем от точки O именно 6 единичных отрезков и получаем искомое расстояние.
Рациональные числа
С действительным числами всё понятно, а что делать с рациональными? Представим, что координаты точки A равны 5,5. Из этого следует, что нам нужно отложить из точки O сначала 5 единичных отрезков, то есть, целое число, а после прибавить 0,5. Иногда это кажется невозможным, ведь некоторые числа трудно представить в виде отрезка, из-за чего приходится искать самое приближенное значение числа.
Иррациональные числа
Иррациональным числам данный метод не подходит, потому как такие числа нельзя поставить на координатной прямой OX. Для примера приведём числа √5, √8, √17. Здесь можно перейти к отвлечённому представлению и посмотреть на эти числа таким образом:
- 0>A – если 0 больше A, то A имеет отрицательное значение координат: |OA| = (–A).
- 0<A – если 0 меньше A, то A имеет положительное значение координат: |OA| = (A).
Также можно сказать, что это подходит и к действительным числами. Если точка A будет находиться на начальной точке O, то и расстояние между ними будет равно 0. Здесь нужно уметь хорошо работать с рисунком, тогда всё будет понятно.
- Модуль
Важно помнить, что расстояние между точками не может быть отрицательным.
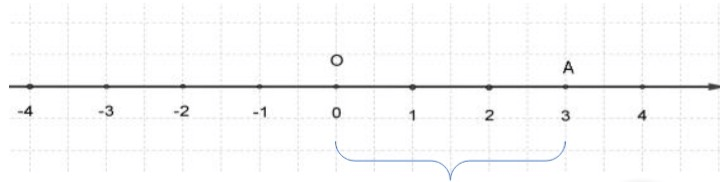
В данном случае у нас есть модуль числа A, что является расстоянием OA и это число 3.
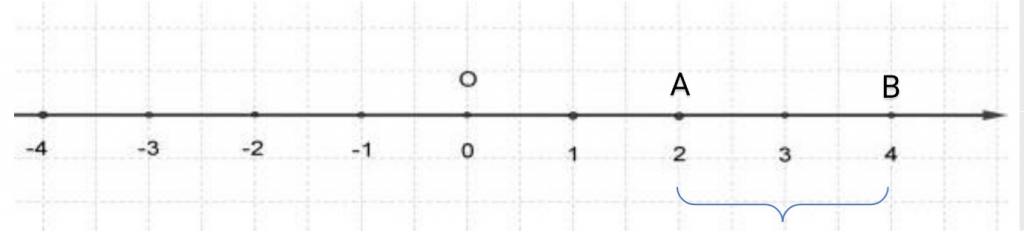
Если на координатной прямой будут точки A и B, то их расстояние нужно определить по модулю разности этих координат. Получается, чтобы найти длину отрезка AB, необходимо из числа точки B отнять число точки A:
4-2=2.
Как определить расстояние между двумя точками на плоскости
Представим прямоугольную систему координат и плоскость на ней, с находящимися там точками A и B. Далее проведём прямые от этих точек к осям Ox и Oy, как на изображении. В следствие этого образовались точки Ax и Ay, а также Bx и By.
Из этого можно вывести несколько вариантов:
- Ось Ox
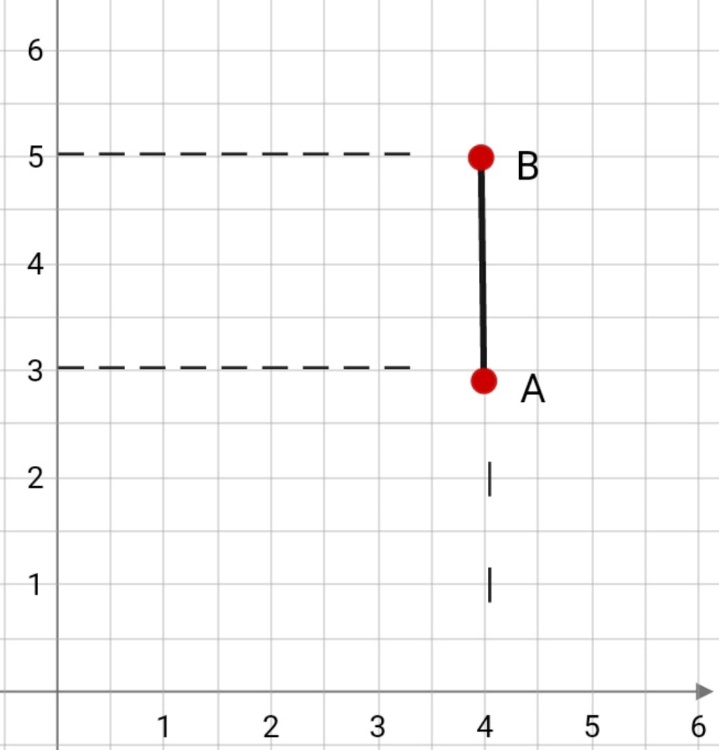
В случае расположения точек A и B на прямой, которая в свою очередь перпендикулярна оси Ox – точки A и B совпадают, а модуль AB равен модулю AyBy. Как говорилось ранее, для нахождения длины промежутка (расстояния) между двумя точками, нужно найти разность модуля заданных координат, поэтому можно сказать, что:
|AB| = |AyBy| = |yB – yA|.
При этом совпадении их расстояние равняется 0.
Формула для нахождения расстояния между двумя точками на плоскости:
\[|A B|=\sqrt{(} x B-x A)^{2}+(y B-y A)^{2}=\sqrt{0}^{2}+(y B-y A)^{2}\]
- Ось Oy
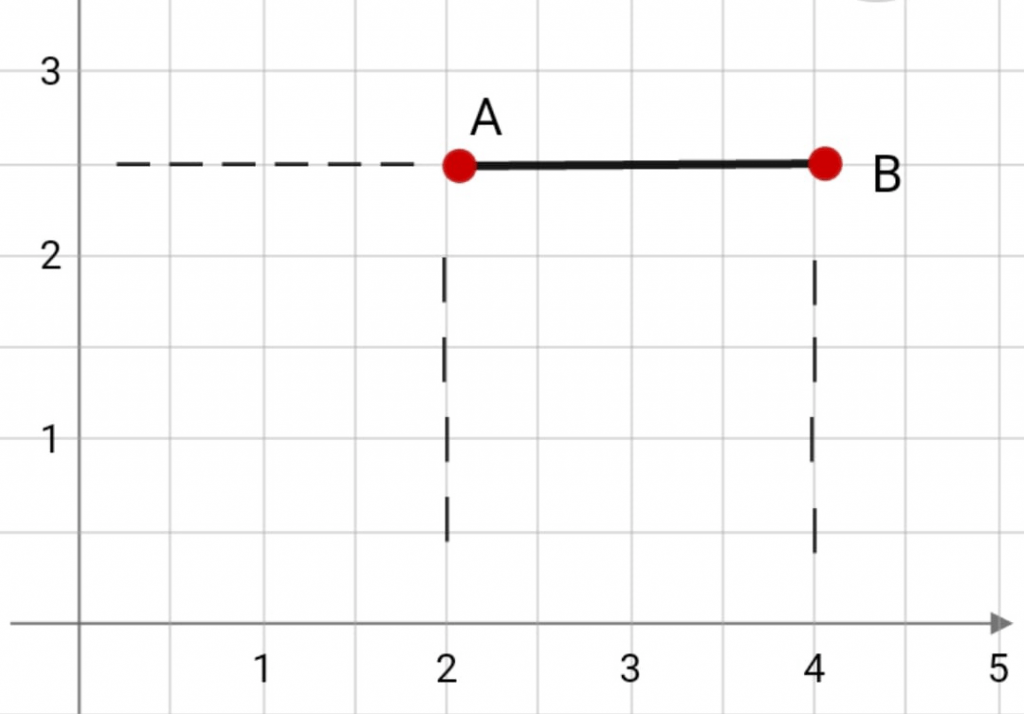
Теперь рассмотрим тот случай, когда прямая перпендикулярна оси Oy. Находится расстояние таким же образом, но уже с участием xB и xA: |AB| = |AxBx| = |xB – xA|.
Формула для нахождения расстояния между двумя точками на плоскости:
\[\left.|A B|=\sqrt{(} x B-x A)^{2}+(y B-y A)^{2}=\sqrt{(} x B-x A\right)^{2}+0^{2}\]
- Точки не лежат на прямой, которая перпендикулярна оси Ox и Oy
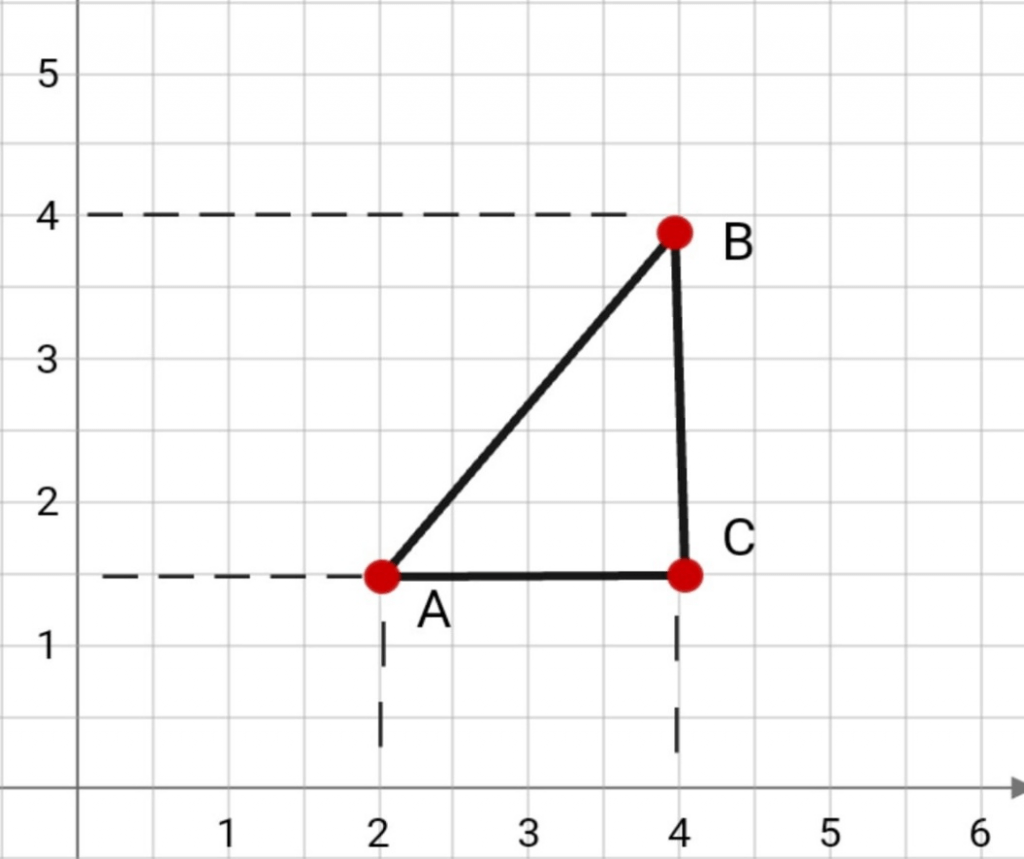
Теперь поговорим о прямоугольном треугольнике ABC. Чтобы найти расстояние на плоскости между точкой A и точкой B, необходимо воспользоваться формулой:
|AB| = √(xB – xA)² + (yB – yA)².
Эта формула доказывает правильность ранее написанных утверждений к тем заданиям, на графиках которых точки лежат на прямой, перпендикулярной Ox и Oy.
Если точки совпадают, к ним справедливо равенство:
|AB| = √(xB – xA)² + (yB – yA)² = √0² + 0² = 0.
По рисунку видно, что:
|AC| = |AxBx|, а также |BC|=|AyBy|. Далее вспомним теорему Пифагора и с её помощью запишем равенство:
|AB|² = |AC|² + |BC|²
|AB|² = |AxBx|² + |AyBy|²
√|AxBx|² + |AyBy|²
√|xB – xA|² + |yB – yA|²
√(xB – xA)² + (yB – yA)²
Пример
Найдите расстояние между двумя точками на плоскости, если известно, что они находятся на прямоугольной системе координат со значениями: A (3, –1), а также B (X + 3, 7). Также надо найти значение действительного числа X, зная, что при них расстояние между точками будет равно 10.
Чтобы решить эту задачу, необходимо использовать формулу:
|AB| = √(xB – xA)² + (yB – yA)².
После этого действия подставляем вышеприведённые числа:
√(X + 3 – 3)² + (7 – ( – 1))² = √X² + 64.
Далее обратим внимание на то, что |AB| = 10 и составим равенство:
√X² + 64 = 10
X² + 64 = 100
X = ± 6
Ответ: |AB| = 10, при X = ±6.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Как определить расстояние между точками в пространстве
Более сложным заданием на нахождение расстояния является то, где точки расположены в пространстве, а не на плоскости.
Возьмём точки, имеющие свои координаты: A (xA, yA, zA), B (xB, yB, zB). Они размещены на прямоугольной системе координат Oxyz. Имея эти данные, мы можем приступить к поиску расстояния между этими точками.
Итак, проведём плоскости через наши точки A и B, которые должны быть перпендикулярными осям с заданными координатами. Таким образом мы получаем точки точки проекции: Ax, Ay, Az, Bx, By, Bz. Так и получился параллелепипед, диагональ которого равна расстоянию точек.
Для нахождения диагонали нужно вспомнить, что она находится путем сложения квадратных измерений точек проекции:
\[|A B|^{2}=|A x B x|^{2}+|A y B y|^{2}+\left.|A| z B z\right|^{2}\]
После чего выполним такие действия:
|AxBx| = |xB – xA|
|AyBy| = |yB – yA|
|AzBz| = |zB – zA|
Теперь выполним преобразование получившегося выражения:
|AB|² = |AxBx|² + |AyBy|² + |AzBz|² = |xB – xA|² + |yB – yA|² + |zB – zA|² = (xB – xA)² + (yB – yA)² + (zB – zA)².
После всех этих действий мы можем выделить основную формулу, которая применяется для нахождения расстояния точек в пространстве:
=√(xB – xA)² + (yB – yA)² + (zB – zA)².
Её можно применять в тех случаях, когда точки располагаются на прямой, которая параллельна координатной оси или же они находятся на этой координатной оси. При совпадении точек эта формула также действительна.
Пример
Найдите расстояние между точками, которые лежат на прямоугольной системе координат в трёхмерном пространстве, координаты которых: A (2, 3, 4), а также B (-6, -1, 5).
Перейдём к решению, воспользовавшись формулой:
√(xB – xA)² + (yB – yA)² + (zB – zA)².
Подставляем имеющиеся значения:
√(–6 – 2)² + (–1 – 3)² + (5 – 4)² = √64 + 16 + 1 = √81 = 9.
Ответ: расстояние |AB| равно 9.
Задачи для самостоятельного решения
- Задача
Найдите расстояние между точками на плоскости, если известно, что они находятся на прямоугольной системе координат со значениями: A (2, 5), а также B (6, 4). - Задача
Найдите расстояние между точками на плоскости, если известно, что они находятся на прямоугольной системе координат со значениями: A (1, 6), а также B (1, 25). - Задача
Найдите расстояние между точками, которые лежат на прямоугольной системе координат в трёхмерном пространстве, координаты которых: A (1, -3, 4), а также B (4, 1, 4). - Задача
Найдите расстояние между точками, которые лежат на прямоугольной системе координат в трёхмерном пространстве, координаты которых: A (2, -2, 7), а также B (6, 2, 5).
Ответы с решением:
- Решение первой задачи
Для решения понадобится формула:
|AB| = √(xB – xA)² + (yB – yA)².
Далее подставляем числа:
|AB| = √(6 – 2)² + (4 – 5)² = √4² + (–1)² = √16 + 1 = √17.
Ответ: |AB| равен √17. - Решение второй задачи
Формула для нахождения:
|AB| = √(xB – xA)² + (yB – yA)².
Подставляем:
|AB| = √(1 – 1)² + (25 – 6)² = √(0)² + (19)² = √0 + 361 = √361 = 19
Ответ: |AB| равен 19. - Решение третьей задачи
Запишем формулу:
√(xB – xA)² + (yB – yA)² + (zB – zA)².
Подставим числа:
√(4 – 1)² + (1 – (–3))² + (4 – 4)² = √(3)² + (4)² + (0)² = √9 + 16 + 0 = √25 = 5.
Ответ: |AB| равняется 5. - Решение четвертой задачи
Записываем формулу для решения:
√(xB – xA)² + (yB – yA)² + (zB – zA)²
Заменим на координаты точек:
√(6 – 2)² + (2 – (–2))² + (5 – 7)² = √(4)² + (4)² + (–2)² = √16 + 16 + 4= √36 = 6.
Ответ: |AB| равняется 6.















