Что такое векторное произведение
Векторное произведение
Для того чтобы дать правильное определение векторного произведения, необходимо разобраться в следующем моменте: рассмотреть вопрос, касающийся ориентации всей упорядоченной группы векторов. Для всего пространства на координатной плоскости.
Нужно отложить все три вектора от одной конкретной точки в системе. Ориентация для векторов может быть двух направлений:
- правая;
- левая.
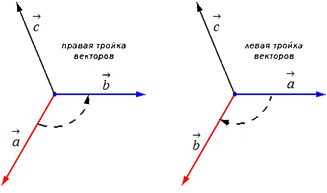
Направление непосредственно зависит от направления самого вектора. Именно в каком направление будет осуществляться самый кратчайший поворот от двух векторов, а и b от конца третьего вектора с. При условии, что самый короткий поворот против часовой стрелки, тогда все три вектора будут именоваться – правыми.
Соответственно левыми будут называться вектора, движение которых происходит по направлению часовой стрелки.
Произведение векторов неколлинеарных векторов \[\bar{a} \text { и } \bar{b} \], которые взятых в определённом порядке – это любой принятый вектор \[\bar{N}\], у которого длина равняется площади геометрической фигуры параллелограмм. Именно он построен на основании данных векторов; вектор \[\bar{N}\] ортогонален двум другим векторам \[\bar{a} \text { и } \bar{b} \], и направлен так, что \[(\bar{a} ; \bar{b} ; \bar{N})\] являются ориентированы в правом направлении.
Следовательно, можно выделить следующие основные моменты:
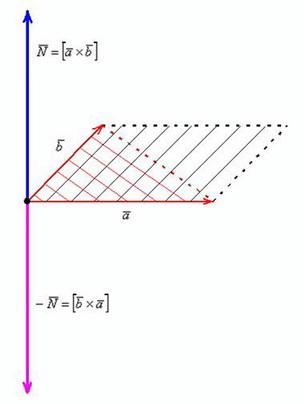
1. Заданные векторы, которые обозначены линиями красного цвета, и основываясь на определение являются не коллинеарными
2. Векторы \[\bar{a} \text { и } \bar{b}\] приняты в заданном порядке: произведение \[[\bar{a} \times \bar{b}]_{-}\]
Окончательный результат выражен как: \[\bar{N}=[\bar{a} \times \bar{b}]\], обозначенный синим цветом.
Если вектора перемножить в обратном порядке, получится равный по всей длине и противоположный по направлению вектор \[-\bar{N}=[\bar{b} \times \bar{a}]\].
Следовательно: \[[\bar{a} \times \bar{b}]=-[\bar{b} \times \bar{a}]\]
3. Геометрический смыл векторного произведения.
Величина длины синего вектора \[\bar{N}=[\bar{a} \times \bar{b}]\] (следовательно это справедливо и для красного вектора \[-\bar{N}=[\bar{b} \times \bar{a}]\]) будет равна площади параллелограмма. Который построен на векторах \[\bar{a} \text { и } \bar{b}\]. На схеме, данная фигура изображена штриховкой черного цвета. чёрным цветом.
Исходя из вышесказанного, справедливой будет формула определения длины для векторного произведения:
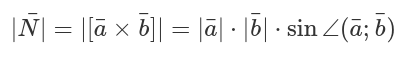
Данная формула отражает длину вектора а не его самого \[\bar{N}\]. Для задач геометрии площадь параллелограмма зачастую определяют через главное понятие произведения векторов:
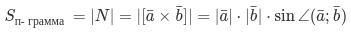
Выведем следующую формулу. Диагональ у параллелограмма (красная пунктирная линия) делит фигуру два равных треугольника.
Из этого следует, что площадь треугольника, который построен на векторах \[\bar{a} \text { и } \bar{b}\], определяется по формуле:
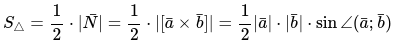
4. Стоит помнить, что вектор \[\bar{N}\] ортогонален векторам \[\bar{a} \text { и } \bar{b}\], иными словами \[\bar{N} \perp \bar{a}, \bar{N} \perp \bar{b}\].
Векторное произведение коллинеарных векторов
Случаи, при которых векторы являются коллинеарными:
- когда вектора возможно расположить на одной прямой;
- параллелограмм визуально, также становится плоским относительно оси координат;
- площадь параллелограмма равна нулю \[S_{\text { п-грамма } }=|\bar{a}| \cdot|\bar{b}| \cdot \sin \angle(\bar{a} ; \bar{b})\](синус нуля равняется или 180 градусов равняется нулю следовательно и площадь также будет нулевой).
Поэтому , если \[\bar{a} || \bar{b} \text {, то } \bar{N}=[\bar{a} \times \bar{b}]=\overline{0} \text{ и }|\bar{N}|=|[\bar{a} \times \bar{b}]|=0\].
Нужно всегда помнить, что именно само векторное произведение равно нулю.
При решении практических задач данным моментом часто пренебрегают.
Пример частного случая \[[\bar{a} \times \bar{a}]=\overline{0}\].
Векторное произведение помогает определить коллинеарность векторов трехмерного типа.
Главные свойства векторного произведения
Для некоторых произвольных векторов \[\bar{a}, \bar{b}, \bar{c}\] и произвольного значения числа \[\lambda\], являются справедливыми следующие главные свойства:
- \[[\bar{a} \times \bar{a}]=\overline{0}\] — данное свойство обычно не выделяют. Однако именно оно является важным моментом процессе решения векторных задач.
- \[[\bar{a} \times \bar{b}]=-[\bar{b} \times \bar{a}]\] – это свойство часто называют анти коммуникативным. Иными словами, порядок векторов может иметь разное направление и значение.
- \[[\lambda \bar{a} \times \bar{b}]=\lambda[\bar{a} \times \bar{b}], \quad[\bar{a} \times(\lambda \bar{b})]=\lambda[\bar{a} \times \bar{b}]\] – суммарные и ассоциативные законы для векторных произведений. Константа выносится за пределы векторного произведения в координатной оси.
- \[[(\bar{a}+\bar{b}) \times \bar{c}]=[\bar{a} \times \bar{c}]+[\bar{b} \times \bar{c}], \quad[\bar{a} \times(\bar{b}+\bar{c})]=[\bar{a} \times \bar{b}]+[\bar{a} \times \bar{c}]\] – распределительные или действующие законы векторного произведения. Для решения главным моментом является умение правильно раскрывать значение в скобках.
Коллинеарные и компланарные векторы. Основные определения
Компланарные вектора — это вектор или несколько векторов, которые расположены на одной плоскости либо располагаются параллельно ей.
Компланарность характерна всегда двум любым, на выбор, векторам. Так как всегда можно вычистить плоскость, которой будет параллельны произвольные вектора.
Выведем основное правило признака копланарности вектора.
При условии, что два вектора a и b не характеризуются как календарные, а для вектора с свойственны только одна пара чисел x и y. c=xa+yb. Если соблюдаются данные условия, то перечисленные векторы можно назвать компланарными.
Обратное утверждение компланарности.
Когда вектора a , b , c — компланарны, при этом a , b не относятся к коллинеарным. можно вектор c разложить по двум любым векторам, только одним способом.
Коллинеарность векторов это — принцип соотношения параллельности векторов. Два вектора с нулевым значением, будут иметь коллинеарность, при условии, что они находятся лежат на параллельной прямой или на одной плоскости с ней.
Главные условия и класс компланарности векторов
- Если произведение трех векторов равно нулевому значению. Данные вектора можно характеризовать как компланарные.
- Когда три любых вектора независимы друг от друга, то они будут компланарными.
- Когда задано несколько векторов, выполняется условие: компланарность будет характерна, для двух любых векторов, если они линейно друг от друга зависимы.
Для более лучшего восприятия материала, необходимо применить правила компланарности и коллинеарности при решении практических задач.
Для этого решим, и подробно распишем три конкретных примера.
Пример №1:
В условии задачи даны три вектора со следующими числовыми значениями.
a(1,2,3);
b(1,1,1);
c(1,2,1).
При условии, что произведение векторов будет равняться нулевому значению, можно сделать вывод о компланарности векторов.
Определяем произведение заданных значений.
Запишем все значения в виде матрицы и решим ее, применяя правила произведения и разности чисел.
a, b, с = 1*1*1+1*2*3+2*1*1-1*1*3-2*1*1-1*2*1=2 0
Так как окончательный ответ не равен нулю, а равен значению два. Следует, что вектора не являются компланарными.
Пример №2:
Заданы три вектора с положительными и отрицательными значениями. Необходимо составить и решить матрицу чисел.
a(1,-1,2);
b(0,1,-1);
c(2,-2,4).
Для решения задачи, нужно вычислить произведение значений векторов.
a, b, с=1*1*1+0*(-2)*2+(-1)*(-1)*2-2*(-1)*1-0*(-1)=0
Выполнив все действия по вычислению произведения данных, мы видим, что ответ уравнения равен нулю.
Согласно основному правило компланарности, можно сделать вывод, что вектора ему соответствую. То есть являются компланарными между собой.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Примеры решения
Для решения некоторых категорий задач, необходимо пользоваться тригонометрической таблицей. Для определения углов функций.
Пример 1:
- Необходимо определить длину векторного произведения двух векторов \[\bar{a} \text { и } \bar{b}\], , если:
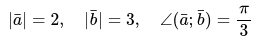
- Определить площадь параллелограмма, который построен на основании векторов \[\bar{a} \text { и } \bar{b}\], если:
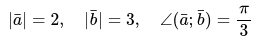
По условию задачи необходимо вычислить длину векторного произведения. По следующей формуле:
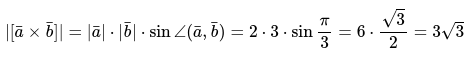
Ответ:

В ответе обязательно следует указывать единицы измерения, так как определится длина.
Из условия задачи нужно определить площадь фигуры параллелограмм, который построен на векторах \[\bar{a} \text { и } \bar{b}\].
Площадь равняется значению длины векторного произведения:
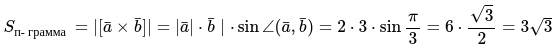
Ответ:
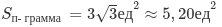
Пример 2:
Определить площадь геометрической фигуры треугольник, который построен на векторах \[\bar{a} \text { и } \bar{b}\], , если:
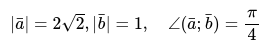
Для решения задачи применим соответствующую формулу и вспомним все преобразования, которые необходимы для определения площади.
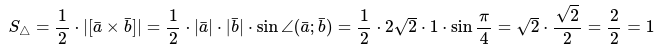
Ответ:
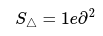
Пример 3:
Найти:
Решение: По условию требуется определить длину векторного произведения:
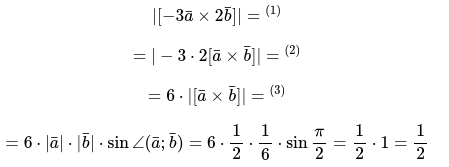
Алгоритм решения:
- вынести за пределы скобок векторного произведения все константы, согласно ассоциативного закона.
- затем выносим значение константы за пределы модуля; при этом модуль изменят отрицательный знак на положительный.
Ответ:
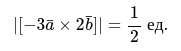
Пример 4:
Необходимо определить значение площади треугольника.
Для этого задано в задаче следующие данные:
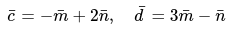
, если:
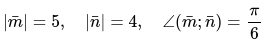
Алгоритм решения задачи:
Площадь треугольника определяется по уже известной формуле:
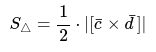
Данный алгоритм стандартный и частично имеет схожесть с другими примерами.
Решение для удобства, необходимо разделить на три этапа:
Этап 1:
Нужно правильно выразим произведение векторов: \[[\bar{c} \times \bar{d}]\] через определение векторного произведения \[[\bar{m} \times \bar{n}]\].
Иными словами, выражение вектора через вектор.
Для этого сформулируем и запишем следующее:
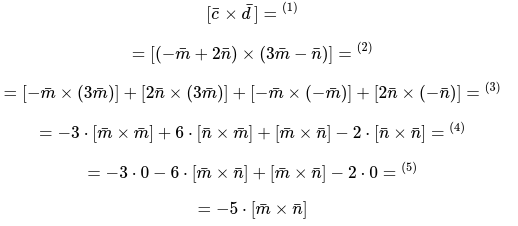
подставляем в формулу соответствующие выражения векторов \[\bar{c}, \bar{d}\].
- используя определённые законы, нужно раскрыть скобки по характерным правилам умножения числовых многочленов.
- применяя ассоциативные векторные законы, можно вынести все константы за скобки и пределы векторных произведений.
Первое и последнее выражение равно нулевому значению или нулевому вектору, исходя из принятого свойства: \[[\bar{a} \times \bar{a}]=\overline{0}\].
Для второго слагаемого применяется свойство анти коммутативности и выглядит следующим образом: \[6 \cdot[\bar{n} \times \bar{m}]=-6 \cdot[\bar{m} \times \bar{n}]\]
— приведение подобных слагаемых.
По результатам вычисления заданный вектор получился выражен через вектор. Этого и требовалось доказать:
\[[\bar{c} \times \bar{d}]=-5 \cdot[\bar{m} \times \bar{n}]\]
Этап 2:
На втором этапе определяется длина заданного векторного произведения.
Приведенное действие напрямую напоминает задачу №3:
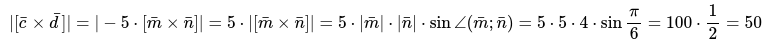
Этап 3:
Применяя все известные данные и формулы, можно определить площадь треугольника:
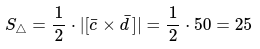
Ответ:
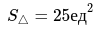
Пример 5:
Определить векторное произведение, применяя все заданные значения векторов:
\[|[\bar{c} \times \bar{d}]|\], если:
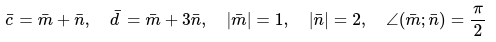
Необходимо выразить вектор \[[\bar{c} \times \bar{d}]\] через другой вектор \[[\bar{m} \times \bar{n}]\]:
Используя все данные и алгоритм решения можно составить формулу и записать следующее выражение подставляя числа:
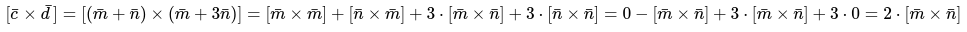
Окончательным действием будет определение произведения векторов, поэтапно подставляя все числовые значения:
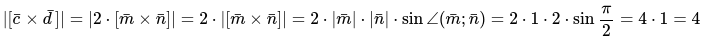
Ответ задачи: \[|[\bar{c} \times \bar{d}]|=4 \text { ед }\]
Векторное произведение векторов в системе координат
Произведение векторов \[\bar{v}\left(v_{1} ; v_{2} ; v_{3}\right), \bar{w}\left(w_{1} ; w_{2} ; w_{3}\right)\], заданные в координатной системе базиса \[(\bar{i} ; \bar{j} ; \bar{k})\],
характеризуются соответствующей формулой:
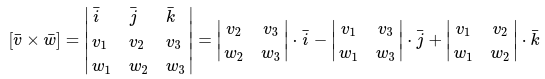
Формула достаточно проста и понятна для восприятия: в верхней строке определителя указываются координатные значения векторов.
Во второй и третьей строке указываются векторные координаты, при этом обозначены в строгом порядке:
- для начала координаты векторов номер 1;
- затем координаты вектора номер 2.
Когда векторы необходимо перемножить в ином порядке, то необходимо все строки поменять с друг другом местами:
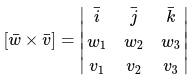
Основываясь на свойства определителя, можно выделить следующее: в случае, когда в определителе две строки нужно поменять местами, то, следовательно, изменится знак
Данное значение определителя всегда отражается в первой строке, что и указано выше.
Пример 7:
Даны следующие данные векторов:
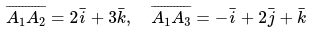
Необходимо определить произведение векторов \[\left[\overline{A_{1} A_{3}} \times \overline{A_{1} A_{2}}\right]\] и вычислить \[\left|\left[\overline{A_{1} A_{3}} \times \overline{A_{1} A_{2}}\right]\right|\]
Используя алгоритм решения выполним следующие действия:
- Сформулируем и запишем формулу для нахождения векторного произведения
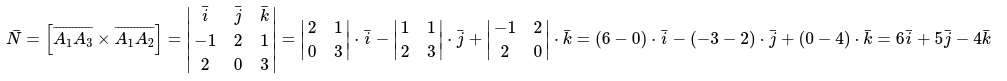
- Подставим имеющиеся данные и вычислим длину векторов по следующей формуле:
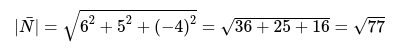
Окончательный ответ:
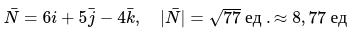
Смешанное произведение векторов
Смешанное произведение применяется довольно редко, поэтому и примеров задач не много.
Практически вся информация сводится к следующим данным:
- главному определению;
- геометрическому смыслу;
- рабочие формулы.
Смешанным произведение нескольких векторов, будет называться произведение трёх характерных векторных значений:
\[(\bar{a} \cdot \bar{b} \cdot \bar{c})\]
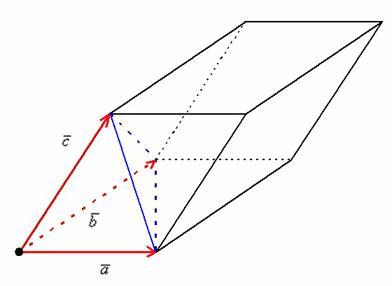
Смешанное произведение трех векторов \[(\bar{a} \cdot \bar{b} \cdot \bar{c})\] и некомпланарных векторов \[\bar{a} \cdot \bar{b} \cdot \bar{c}\], которые берутся в определенном порядке, будет называется объём геометрического параллелепипеда.
Данная геометрическая фигура построена на заданных векторах, которые отражены с положительным значением.
Если базисное значение векторов \[(\bar{a} \cdot \bar{b} \cdot \bar{c})\] имеет правое направление , когда отрицательный знак, то базис векторов \[(\bar{a} \cdot \bar{b} \cdot \bar{c})\] имеет левое направление.
Все характеристики подробно изображены на рисунке.
Смешанное произведение векторов в координатах
Для данного способа определения произведения векторов, используется сугубо алгебраический метод.
Перечень смешанных векторов: \[\bar {v}\left(v_{1}, v_{2}, v_{3}\right), \bar{w}\left(w_{1}, w_{2}, w_{3}\right), \bar{s}\left(s_{1}, s_{2}, s_{3}\right)\], которые непосредственно заданы в координатной системе данных \[(\bar{i} ; \bar{j} ; \bar{k})\] для правого направления, следует выражать характерной формулой, виде матрицы:
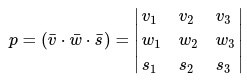
Ориентация базиса – это его стандартная ориентация, для которой решаются практически все задачи.
С практической точки зрения стоит отметить следующие важные моменты:
- для всего векторного произведения, координатные данные векторов следует изображать в конкретный определитель в особо строгом порядке.
- когда в любом смешанном произведении \[(\bar{v} \cdot \bar{w} \cdot \bar{s})\] выбрать несколько векторов, затем переставить их местами, следовательно нужно переставить и все характерные строки определителя.
- при перестановке строк в количестве двух штук, соответствующие строки изменяют знак на противоположный.
- при перемене местами любых векторов, для смешанного произведения будет характерно изменение знака на противоположный.
Соответственно, все координаты векторов не всегда нужно записывать в виде строк. Также они могут изображаться как таблица: слева направо, и обязательно, в строгом порядке.
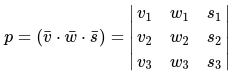
Основное значение главного определителя при этом изменяться не будет: компланарность векторов также имеет огромное значение в данном случае.
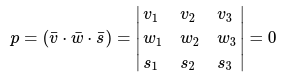
Пример 1
Даны следующие значения векторов \[\bar{a}(1 ;-1 ; 2), \bar{b}(0 ; 4 ; 3), \bar{c}(3 ; 2 ;-6)\].
Необходимо определить:
- смешанное векторное произведение;
- значение объема параллелепипеда, который построен на векторах \[\bar{a}, \bar{b}, \bar{c}\];
- значение объёма геометрической фигуры тетраэдра, который также построен на векторах \[\bar{a}, \bar{b}, \bar{c}\].
Процесс решения заключается в следующем
1. Применяя формулу для смешанного произведения вычисляем неизвестную:
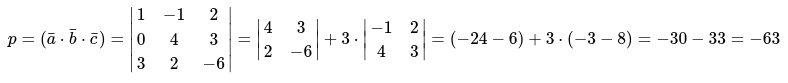
Значение определителя раскрыто по первому столбцу
2. Определение значения объёма параллелепипеда, который построен на векторах \[\bar{a}, \bar{b}, \bar{c}\], равняется модулю смешанного векторного произведения:
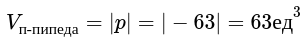
3. Определяем значение объема тетраэдра, который построен на заданных векторах:
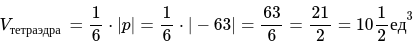
Ответ:
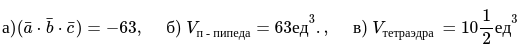
Пример 2
Определить значение объема, которое характерно для треугольной пирамиды. Применяя все известные ее вершины: A(-2 ;-2 ; 0), B(0 ; 4 ;-1), C(1 ; 2 ; 1), D(-13 ; 8 ; 11)
Решение: Для простоты выполнения, рекомендуется выполнять схематический рисунок геометрической пирамиды, это необходимо для более понятного процесса решения.
Для начал определяются значения векторов, по исходным данным:
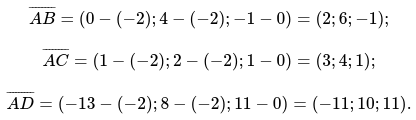
Следующим действием произведение векторов смешанного типа.
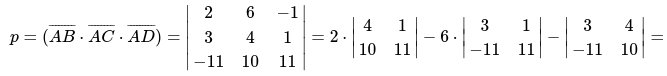
Выполним расчет для треугольной пирамиды ABCD:
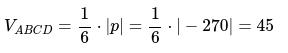
Ответ задачи: \[V_{A B C D}=45 \mathrm{ед}^{3}\]
Пример 3
Определить объём заданной пирамиды, с известными вершинами: \[A_{1}(2 ;-1 ; 3), A_{2}(-5 ; 1 ; 1), A_{3}(0 ; 3 ;-4), A_{4}(-1 ;-3 ; 4)\]
Для начала определим значения векторов
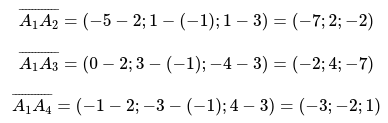
Смешанное произведение определим по формуле:
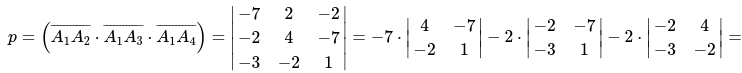
Применяя формулу из геометрии определим объем пирамиды \[A_{1} A_{2} A_{3} A_{4}\]
\[V_{\text {пир}}=\frac{1}{6} \cdot|p|=\frac{1}{6} \cdot 84=14\text{ед} .^{3}\]
\[V_{\text {пир}}=14\text{ед} .^{3}\]















