Вычитание векторов. Как найти разность векторов
Для того, чтобы уяснить, что собой представляет разность векторов, введём понятие откладывания вектора от определённой точки и понятие суммы векторов.
Если некоторая точка A является началом вектора a, то говорят, что он является отложенным от точки A.
Теорема. От каждой точки можно отложить только один вектор, имеющий заданный модуль и направление. Докажем эту теорему.
Доказательство:
В случае, когда вектор нулевой, то теорема очевидна. Нулевые вектора в одной и той же точки совпадают между собой, т. е. являются одним и тем же вектором.
Сделаем построение. Точкой A обозначим начало вектора a, а точкой B его конец. Пусть у нас имеется некоторая точка K. Проведём через неё прямую b, которая параллельна вектору a. Отложим на данной прямой равные по своей абсолютной величине вектору a отрезки KL и KM. Из векторов, образованных этими отрезками искомым можно назвать только сонаправленный с a.
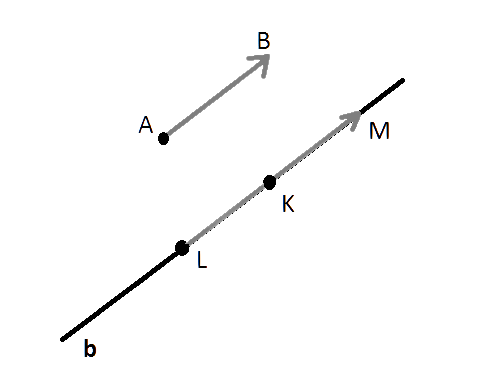
Единственность нашего вектора следует из того, что мы построили и видим.
Теорема доказана.
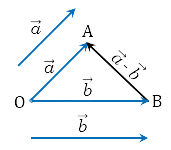
Суммой векторов a и b называется вектор с тем же началом, что вектор a и концом, как у вектора b. При этом вектор b должен начинаться в той же самой точке, в которой заканчивается вектор a.
Равные векторы, начинающиеся в разных точках, нередко обозначают одной и той же буквой. Иногда про подобные векторы говорят, как об одном и том же векторе, отложенном из разных мест.
Разность векторов
Разностью векторов a и b называется сумма вектора a c вектором, который противоположно направлен к вектору b.
По-другому это определение можно сформулировать следующим образом: разностью двух векторов a и b называется вектор c, который при сложении с вычитаемым b образует уменьшаемое, т. е. вектор a.
Формулами это записывается так:
b + c = a
a – b = c
Как найти разность векторов аналитическим способом
В двухмерном пространстве векторов a {x1, y1} и b {x2, y₂} разность векторов можно вычислить, как показано ниже:
c {x3, y3} = {x₁ — x2, y1 — y₂}.
Вычитание векторов в 3-мерном пространстве выглядит следующим образом:
c {x3; y3; z₃} = {x₁ — x2, y₂ — y₂, z1 — z2}.
Как найти разность векторов графическим способом
Нужно воспользоваться правилом треугольника. Последовательность действий следующая:
- Постройте по координатам векторы, для которых требуется найти разность;
- Совместите концы построенных векторов. Для этого нужно построить два равных заданным направленных отрезка, концы у которых будут в одной и той же точке;
- Соедините начала построенных отрезков и укажите их направление. Вектор c, называемый разностью векторов, будет иметь своё начало в той же точке, где начинается вектор, именуемый уменьшаемым и заканчивается в точке начала вычитаемого. Смотрите рисунок ниже.
Есть ещё один способ графического нахождения разности векторов. Он предусматривает следующий порядок действий:
- Постройте исходные направленные отрезки;
- Отразите вычитаемый отрезок. Для этого постройте противоположно направленный и равный ему отрезок и затем совместите начало этого отрезка с уменьшаемым;
- Постройте сумму, т. е. соедините начало первого отрезка и конец второго.
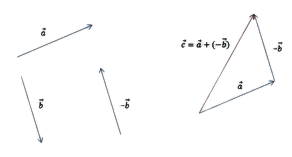
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Примеры вычисления разности векторов
Вычислить вектор c, который представляет собой разность вектора a ={1;
2} и вектора b = {4; 8}.
Решение:
Действуем по выше указанному правилу
a — b = {1 — 4; 2 — 8} = {-3; -6}
Ответ: с{-3; -6}.
Вычислить вектор c, который является разностью векторов a = {1; 2; 5} и
b = {4; 8; 1}.
Решение:
Почти всё делается, как в уже рассмотренном примере, только добавляется третья координата.
a — b = {1 — 4; 2 — 8; 5 — 1} = {-3; -6; 4}
Ответ: c {-3; -6; 4}.
На рисунке векторы
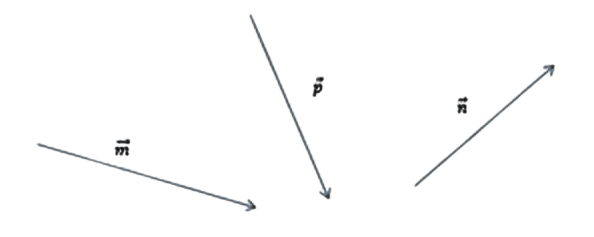
Требуется построить разности: p — n, m —
n,m — n — p и найти ту из них, которая
имеет наименьший модуль.
Решение:
Для изображения p — n проще всего воспользоваться правилом треугольника. Параллельным переносом
отрезки
следует соединить таким образом, чтобы совпали их конечные точки. Далее нужно соединить начальные точки и
определить направление. В нашем случае вектор разности берёт своё начало там же, где и вычитаемый n.
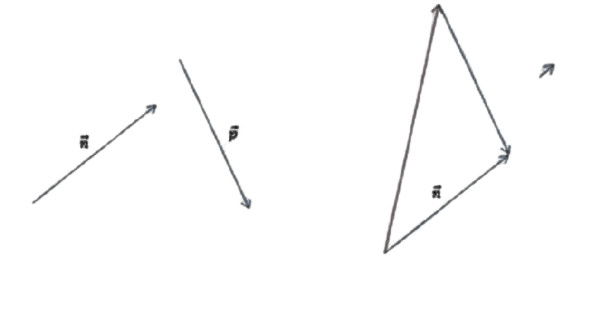
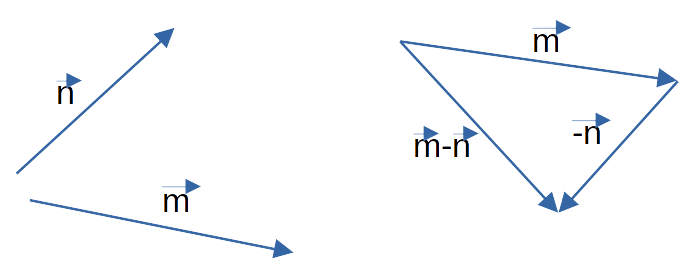
Для изображения m — n правильнее будет воспользоваться вторым графическим способом нахождения разности
векторов. Сначала построим вектор противоположный n и найдём его суммы с вектором m.
Для нахождения разности m — n — p разобьём это выражение на два действия. Возможны следующие варианты:
- m — (n + p). Сначала нужно построить сумму,
затем уже вычесть её из m; - (m — n) — p. Сначала находим m — n,
осле этого от полученной разности отнимаем p; - (m— p) — n. Сначала определяем m — p, затем от
полученного результата отнимаем n.
Из вычислений выше нам известна разность m — n. Для получения решения нам нужно вычесть из неё
p.
Используя определение 3 построим разность векторов на рисунке. На нём изображён окончательный результат
и промежуточный.
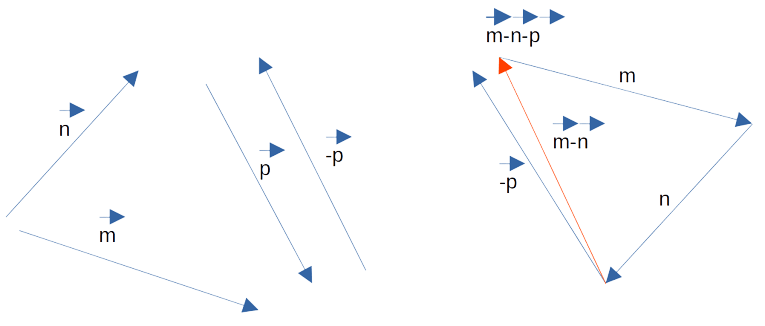
Теперь нужно определить наименьший модуль. В нашем случае для этого можно лишь визуально оценить длины p — n,
m — n и m — n — p. Из построения сразу видно, что наименьшим модулем обладает вектор разности m — n —
p.
Выполнение любых работ по математике
Популярные статьи
Примеры решения матриц с ответами
Общее уравнение плоскости
Метод Крамера – теорема, примеры решений
Нахождение площади фигуры ограниченной линиями y=f(x), x=g(y)