Область допустимых значений (ОДЗ)
Как найти область допустимых значений выражения
Область ОДЗ – это множество простых числовых значений, которые допустимы, для любого данного выражения.
Ограничение области определения:
Область ограничения действительных чисел может быть от \[(0 ;+\infty)\].
Например: \[[-4 ; 1) \cup[5,7)\].
Область определения может указывать на следующие характеристики:
- деление функции как \[y=x+\frac{2 \cdot x}{x^{4}-1}\]
- корень четной степени и переменная под корнем:
\[=\sqrt{x+1} \text { или } y=\sqrt[n]{2^{2 \cdot x+1}} \text {; }\] - переменная в основании степенного значения
\[y=3 \cdot(x+1)^{-2}, y=-2+x^{\frac{1}{3}} ; y=\left(x^{4}-x+2\right)\sqrt{4}\] - логарифмическая переменная \[y=\ln \frac{x^{4}+x}{8} ; \quad y=2+\].
Значения основания должно быть положительным. Также как и логарифмическое значение. - переменная тангенса и котангенса в виде следующего уравнения: \[y=\arcsin (x+4)+4 \cdot x^{2}\]
Если отсутствует хотя бы один из перечисленных характеристик область определения функции определяется иначе.
Пример 1: \[y=\frac{x^{4}+2 x-x+2}{4}+2 \frac{2}{3} \cdot x\], в данном множестве нет переменной, поэтому и решается оно иначе.
Пример 2: \[y=\frac{3}{x-1}\], нужно вычислить область определения. Обязательно, при решении нужно уделить внимание на знаменатель. Потому что, по законам алгебры деление на ноль запрещено.
Следовательно получаем следующее действие: \[\frac{3}{x-1}\].
Область значения не должна быть равной единице, так как в знаменателе получим нулевое значение. Отсюда область определения будет в пределах \[(-\infty, 1) \cup(1,+\infty)\].
Область допустимых значений для уравнения
Чтобы правильно уметь определять данную область, нужно знать следующие утверждения:
если функция вычисляется, при помощи суммы: \[f_{1}+f_{2}+\ldots f_{n} \text { или } \mathrm{y}=f_{1}+f_{2}+\ldots f_{n}\].
Область определения будет следующего вида: \[\mathrm{D}(\mathrm{f})=\mathrm{D}\left(f_{1}\right)\left(f_{2}\right) \ldots\left(f_{n}\right)\]
Пример суммы числовых значений:
Возьмем уравнение: \[y=x^{7}+x+5+\operatorname{tg} x\]
Решение: уравнение представлено в виде суммы нескольких значений, где степень равна семи, показатель один.
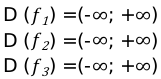
Области определения tg характерны все действительные числа.
Ответ: для заданной функции относится пересечение областей или количество действительных чисел кроме [\pi / 2+\pi \cdot \mathrm{n} . \mathrm{n} \in z]
Пример разности значений:
Решение:
Область определения функции разности будет: \[(0,+\infty)\] это для \[f_{1} ; \text { для } f_{2}(-\infty .+\infty)\]
Ответ: \[(0 ;+\infty)\].
Пример произведения чисел:

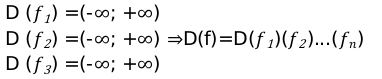
Область допустимых значений для функции
Сложная функция имеет следующий вид: \[\mathrm{y}=f_{1}\left(f_{2}(\mathrm{k})\right)\]
D (f) — множество значений;
Пересечение двух множеств и будет являться областью определения функции сложного типа.
\[y=\ln x^{2}\]
Представим функцию в виде: \[\mathrm{y}=f_{1}\left(f_{2}(\mathrm{k})\right)\]
\[f_{1}\] — логарифм с заданным основанием;
\[f_{1}\] — степень со значением 2.
Используем изученные в данном уроке области определения:
\[D\left(f_{1}\right)=(0 ;+\infty)\]
\[D\left(f_{2}\right)=(-\infty ;+\infty)\]
Исходя из этого получаем систему неравенства: \[x \in D\left(f_{2}\right) ; f_{2} k \in D\left(f_{1}\right) \Leftrightarrow k \in(-\infty ;+\infty) k^{2} \in(0 ;+\infty) \Leftrightarrow k \in(-\infty ;+\infty)k^{2}>0 \Leftrightarrow k \in(-\infty ;+\infty)\]
\[ k \in(-\infty ; 0) \cup(0 ;+\infty) . \Leftrightarrow k \in(-\infty ; 0) \cup(0,+\infty)\]
Ответ: все действительные числа, кроме нуля.
Область определения функции в виде дробного алгебраического значения
Когда функция задается выражение в виде дроби. Переменная значений находится в знаменателе. Следовательно, область определения являются действительные числа. Исключением служит число, которое приведет знаменатель к нулевому значению.
Пример №1: \[y=\frac{x-4}{x+4}\]. Решив уравнение, определим искомое значение области определения. Которое является \[-\infty ;-4 \cup-4 ;+\infty\]
Пример №2: \[y=\frac{1}{x^{2^{2}} 1} ;\]
Искомая область : \[\text { — ]- } \infty ;-1[\cup]-1 ; 1[\cup] 1 ;+\infty[.\]
Пример №3: \[y=\cos x+\frac{3}{x^{2}-4}\].
Первое слагаемое имеет область определения множество действительных чисел. Второе — также все числа, кроме -2 и 2, они приведут знаменатель к нулю. Область определения должна соответствовать условиям двух слагаемых и равняться действительным числам, кроме -2 и 2.
Область определения показательной и логарифмической функции
Показательная функция записывается как: \[y=k^{x}\]
где значение x — показатель степени; k — число, которое обязательно больше нуля и не равно единице. Область определения показательной функции — это множество значений R.
Основные примеры показательных функций:
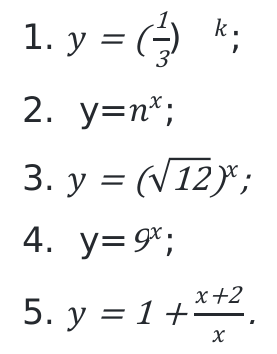
Область определения, для этих функций, записывается следующим образом: \[(-\infty,+\infty)\].
Логарифмическая функция выражается как: \[y=\log n^{k}\], где значение n , имеет значение больше нуля и не менее единицы.
Область определения логарифма и логарифмической функции — это множество положительных значений и действительных чисел.
Рассмотрим на примере, характер решения задачи данной функции.
Пример №1:
\[y=\ln x\], определить область определения натурального логарифма.
На заданном интервале, производная будет иметь положительное значение, и функция будет возрастать на всем промежутке.
Определим односторонний предел при, стремлении аргумента к нулю и когда значение x стремится к бесконечности.
Из данного решения мы видим, что значения будут возрастать от минус бесконечности до плюс бесконечности.
Из этого следует, что множество всех действительных чисел – является областью значений функции натурального логарифма ln.
Ответ: множество всех действительных чисел, это и есть область значений функции ln.
Определения области допустимых значений функции
На примерах рассмотрим, как определить области значений функции.
Первоначально, необходимо определить значения непрерывной функции y=f(x).
Известно, что функция непрерывная и достигает своих максимальных max f(x) и минимальных min f(x) значений, на разных периодах. Из этого следует отрезок, где находятся значения исходной функции. Тогда решение состоит в нахождении точек максимума и минимума.
Пример №1 :
Необходимо вычислить область значений уравнения \[y=x^{4}-5 x^{3}+6 x^{2}\] на отрезке [ 1 ; 4 ] [1; 4].
Для решения задачи необходимо произвести следующие действия:
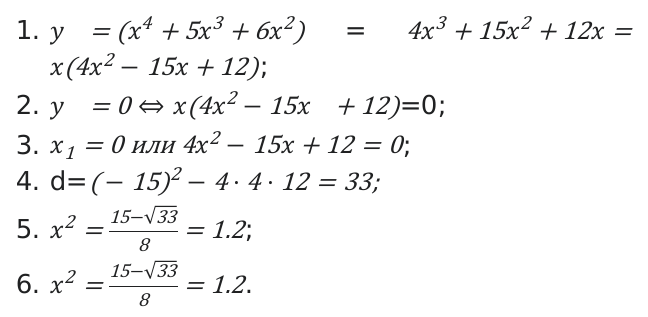
Следующим шагом будет определение значений функции в конечной и начальной точках.
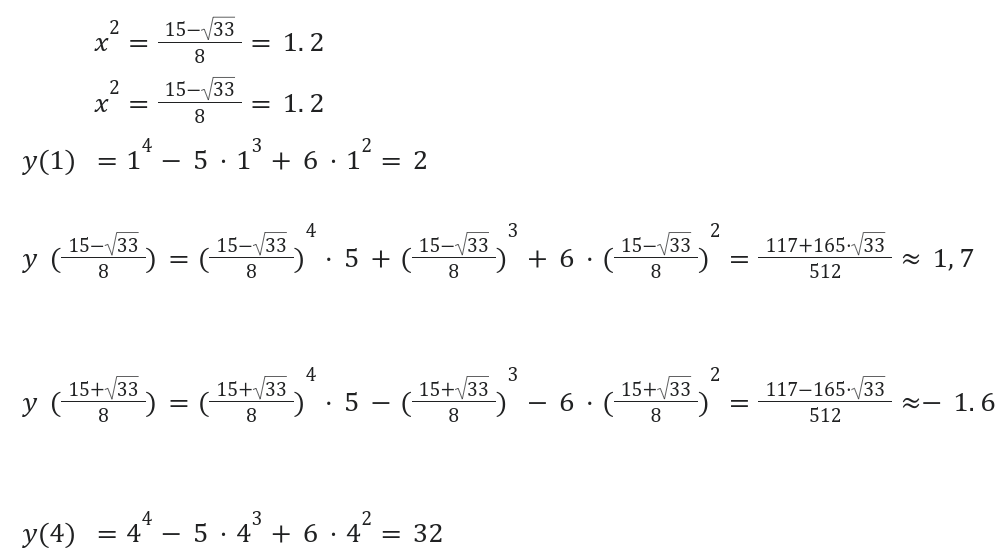
Ответ: \[\left(\frac{117-165 \cdot \sqrt{33}}{512} ; 32\right)\].

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Пример №2.
На этом примере подробно рассмотрим, как вычисляются значения непрерывной функции y= f(x), в определенных промежутках.
Для этого, первоначально вычислим:
- наименьшее и наибольшее значение;
- определим промежуток возрастания и убывания функции;
- односторонние пределы;
- предел бесконечности.
Решение:
Для решения возьмем функцию \[y=\frac{1}{x^{2}-4}\] и вычислим область значений на промежутке (-2;2).
Находим наименьшее и наибольшее значение функции на заданном отрезке.
Из данных вычислений видно, что максимальное значение равно 0, так как в этой точке происходит перемена знака функции и соответственно функция начинает убывать.
А именно: \[y(0)=\frac{1}{0^{2}-4}=-\frac{1}{4}\]
\[-\frac{1}{4}\] — будет являться наибольшим значение заданной функции.
Следующим шагом в нашем решении, будет выяснение направления функции. Когда x значение стремится к (-2) и (+2).
В алгебре иными словами эти значения называют односторонними пределами.
Решение выглядит следующим образом.
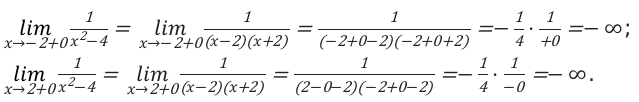
В конечном итоге мы получаем, что в пределах от -2 до 0, функции будут возрастать от \[-\infty \text { до }-\frac{1}{4}\]. Если аргумент меняется, от 0 до то наоборот будет убывать к \[-\infty\].
Следовательно, необходимое множество значений будет на интервале \[-\infty \text { до }-\frac{1}{4}\]
Ответ: \[\left(-\infty-\frac{1}{4}\right)\].
Пример №3:
Данная функция имеет определенное значение, только при положительных значениях. \[\mathrm{D}(\mathrm{y})=(0 ;+\infty)\]
Производная будет иметь следующий вид: \[y=(\ln x)=\frac{1}{x}\].
Так как функция имеет положительное значение, то всем промежутке будет наблюдаться ее возрастание. От \[-\infty \text { до } +\infty\]
Поэтому область значения — это множество всех натуральных значений.
Пример №4:
У функции \[y=\frac{9}{z^{2}-1}\]
Если значение z имеет положительное значение, то функция будет считаться определенной.
Вычислим наибольшее и наименьшее значение, а также промежутки возрастания и убывания.
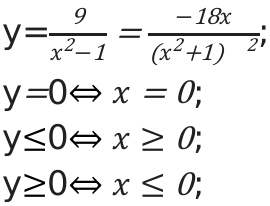
Если значение x будет больше, либо равным 0,то функция будет убывать.
Если значение x будет меньше либо равным нулю , функция будет возрастать.
Затем рассмотрим поведение функции и ее значения на бесконечной прямой.
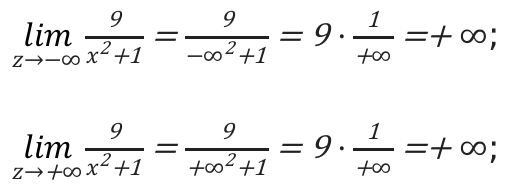
Вывод: если аргумент изменяется от \[-\infty\] до 0, тогда значение функции увеличиваются от 0 до 9 . Когда значения аргумента меняются от 0 до \[+\infty\], значения функции будут уменьшаться от 9 до 0.
Пример №5:
Определить область значений \[y=\frac{x}{x-2}\];
По правилам математики. знаменатель не может равняться нулю. Поэтому: \[D(y)=(-\infty ; 2)(+\infty ; 2)\].
Определим множества на первом отрезке. \[(-\infty ; 2)\]. На этом отрезке функция будет убывающей и значение отрицательным.
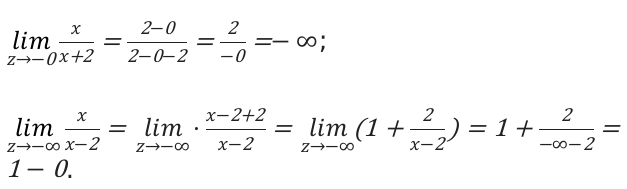
Функция ассиметрично начнет приближаться к 1, когда аргумент будет изменяться к минус бесконечности.
Определим множества на втором отрезке. \[(+\infty ; 2)\]. На этом отрезке функция будет также убывающей.
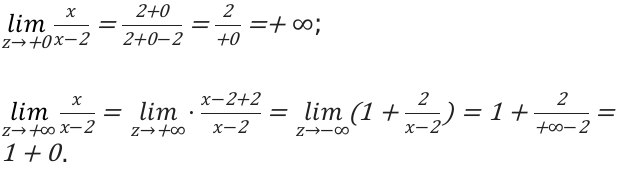
Вывод: \[E(y)=(+\infty ; 1) \cup(1 ;+\infty)\].















