Скобки в математике их виды и предназначение
Открывая математические правила и законы, ученые одновременно с этим разрабатывают знаки, обозначения и символику. Знаки и символы в математике, в том числе, действия в скобках, — условные обозначения, которые применяют при записи специальных понятий, терминов и выражений. Это своеобразный язык, позволяющий максимально упростить и сократить подачу информации, выразить мысль предельно точно, избежать ошибок, двусмысленных трактовок. Скобки — одни из символов, применяемых особенно часто.
Данная статья посвящена применению скобок при решении задач в математике, действия с ними, область их использования, основные разновидности. Приведены основные термины и методы их применения для различных задач. Имеются примеры с разъяснениями.
Математика: действия со скобками различных видов
Скобки — парные (за небольшим исключением) знаки. Первая называется открывающей, вторая — закрывающей. Они отграничивают определенную часть математического выражения, помогая определиться с порядком выполнения действий.
При решении математических задач применяют 3 разновидности скобок: (), {}, []. Используют, но несколько реже, обратные скобки, которые выглядят так:] и [, а также < и > (уголки). Применение этих знаков всегда является парным, то есть математическое выражение включает открывающуюся и закрывающуюся скобки. Только в этом случае выражение имеет смысл. Назначение этих знаков — разграничение действий и определение последовательности их выполнения.
Область применения круглых скобок:
- обозначение выражений, с которыми выполняются те или иные математические действия. Пример — возведение многочлена в степень: \[(c+d)^{3}\] и т. д.;
- указание координат точек в одно- и многомерных системах;
- компактная запись периодических десятичных дробей;
- запись отрицательного числа в математическом выражении с целью разделения знаков математического действия и самого числа.
Круглые скобки помогают определиться с последовательностью и приоритетом логических операций и математических действий (как вариант, для изменения существующего алгоритма).
Квадратные знаки применяют для:
- указания целой части числа;
- взятия модуля числа;
- определения порядка действий, аналогично круглым;
- операций с векторами;
- указания скобок второго уровня;
- записи координат, массивов чисел.
Помимо математики, квадратные скобки применяют при записи физических, химических формул, в программировании.
Фигурные скобки ({) используют при обозначении множеств, для объединения уравнений или неравенств в систему, как скобки третьего уровня. Их также применяют при решении систем уравнений (пересечение множеств), а квадратные — [используют для записи их объединения (так называемые совокупности). Рассмотрим примеры с этими символами более подробно.
Принципы раскрытия, примеры по математике со скобками
Рассмотрим порядок выполнения действий с примерами со скобками в математике, правила их использования.
Правило 1. Если перед скобками поставлен плюс, — знаки чисел, заключенных внутри, остаются
неизменными. Пример: \[4+(5-1-2+3)=4+5-1-2+3\]
Правило 2. Если перед скобками поставлен минус, то знаки чисел, находящихся внутри, при
раскрытии меняются на противоположные.
Пример: \[a-(b+c-k)=a-b-c+k\]
Правило 3. Если перед скобками или после них находится знак «умножение», — получаемый
результат зависит от выполняемых действий.
Примеры:
Примеры с умножением: \[3 \cdot(2 \cdot 4 \cdot 6 \cdot 9)=3 \cdot 2 \cdot 4 \cdot 6 \cdot 9 ;(3 \cdot 2
\cdot 9) \cdot 4=3 \cdot 2 \cdot 9 \cdot 4\]
Примеры с делением: \[3 \cdot(15: 5)=(3-15): 5=(3: 5) \cdot 15 ;(10: 2) \cdot 3=(3 \cdot 10): 2=(3: 2) \cdot
10\]
Правило 4. если перед скобками либо после них поставлен знак «деление», то результат зависит
от того, какие действия выполняют внутри них.
Порядок выполнения действий со скобками в математике
Самое частое использование скобок — указание алгоритма выполнения действий. С этой целью используют круглые символы, одну или несколько пар. Порядок решения — следующий:
- действие в скобках;
- умножение, деление;
- сложение, вычитание.
Пример №1. Если задано выражение 7 + 3 — 1, то действия выполняют последовательно. Порядок действий меняется, если задействовать скобки. Например, в выражении (7 + 3) — 1 вначале выполняют сложение, заключенное в скобки. Результат останется тем же: 9. Если записать выражение, обособив при этом вычитание 7 + (3 — 1), вначале выполняют вычитание в скобках, а затем сложение с числом 7. В данном примере окончательный результат остается тем же.
Пример №2. Рассмотрим, когда от расположения скобок в математическом выражении зависит результат. В выражении \[7+3 \cdot 4\] очевидно, что вначале следует выполнить умножение. Получаем результат 19. Если выражение будет выглядеть как \[(7+3) \cdot 4\], то сначала выполняют сложение в скобках. Конечный результат — 40.
Пример №3. В выражении \[(5 \cdot(8-4)+6): 2\] вначале отнимают 4 от 8. Полученный результат умножают на 5. К произведению прибавляем 6. Последним действием будет деление на 2.
Нередко можно встретить символы различного размера. Делают это из соображений удобства, чтобы упростить порядок действий и переход от одного вычисления к другому. Внутренние скобки всегда меньше внешних. Например, \[\left(\left((7-2): 2+\frac{1}{2}\right)+4-\frac{1}{4} \cdot 5\right) \cdot 3-5\]. Можно также воспользоваться квадратными знаками: \[[4+7 \cdot(4-3)] \cdot 5\]. Или оформить пример символами фигурными: \[{6+[6-12(7-4): 3]+8-4}:[4+7+5:(6-4-1)]\]. Чтобы получить правильный результат, нужно вначале определиться с порядком действий и парами скобок. Чтобы упростить задачу, можно воспользоваться различными их типами или выделять каждую пару «своим» цветом. Последний вариант используется нечасто, так как занимает много времени и попросту неудобен. Использование сочетаний круглых, фигурных и квадратных знаков удобнее.
Скобки в математике и отрицательные числа
Для отображения отрицательных чисел пользуются круглыми символами. Примеры:
Если отрицательное число находится в начале выражения, его не заключают в скобки. Пример: \[-3 \cdot 4+(-8): 2\]. Отрицательное число -3 в начале выражения можно записывать без скобок. Еще один пример: \[\frac{2-1,5}{-2,3 \cdot(4+6)+(5-3): 2}\]. Число -2,3 в знаменателе находится в самом начале, поэтому подобное обособление не является обязательным. Впрочем, можно записать эти же выражения и со скобками. Примеры: \[(-3) \cdot 4+(-8): 2\] или \[\frac{2-1,5}{(-2,3) \cdot(4+6)+(5-3): 2}\]. Такая запись является более строгой, исключающей любые разночтения с алгоритмом выполнения действий.
Со знаком минус могут записываться не только числа, но и степени, корни, функции, дроби. Примеры:
Скобки, используемые для выражений, с которыми выполняют действия
Круглые скобки применяют при записи действий с возведением в степень, функций, производных. Это позволяет определиться с алгоритмом действий и, таким образом, упростить решение задачи. Рассмотрим эти примеры более подробно, по каждому из пунктов.
Скобки в математике и выражения со степенями
Поскольку степень расположена над строкой, скобки при записи используют не всегда. Например, в выражении \[3^{x+2}\] они будут явно лишними, поскольку и так понятно, что выражение \[x+2\] является показателем степени. Скобками придется воспользоваться, если степень записывают с применением знака ^. То же самое выражение будет выглядеть так: \[3 \wedge(x+2)\]. Если пренебречь обособлением, то получатся совершенно иные выражения: \[3^{x}+2\], или \[ 3^{x}+2\].
Основание степени может быть как в скобках, так и без. Примеры, когда в них нет необходимости: \[2^{3} ; 3^{x^{2}+9} ; y^{0,2}\]. Если основанием степени является дробь, то можно воспользоваться круглыми символами: \[(0,95)^{3} ;\left(2 \frac{1}{3}\right)^{x+3} ;(5 \cdot x+3 y)^{-2} ;\left(\log _{3} x-5\right)^{-\frac{1}{5} x}-3\]. Если основание степени не заключить в скобки, то получится совершенно иной результат.
Например, если основанием степени является выражение \[x^{3}+2 y\], а показателем — -2, то степень будет записана таким образом: \[\left(x^{3}+2 y\right)^{-2}\]. Если обособления нет, то выражение примет вид \[\left(x^{3}+2 y\right)^{-2}\], то есть станет совершенно иным.
Если в качестве основания степени используется тригонометрическая функция или логарифм, выражение можно записать как с применением скобок, так и без них. Например, степени \[\sin ^{2} x \text { и }(\sin x)^{2}\] равноценны. Аналогично, тождественны и такие выражения, как \[(\lg x)^{3} \text { и } \lg ^{3} x\].
Выражения, содержащие корни, и скобки
Применять знаки в подкоренном выражении не обязательно. На решение они никак не повлияют. Пример: \[\sqrt{x+2} \text { и } \sqrt{(x+2)}\] — равнозначные выражения.
Выражения с тригонометрическими функциями и скобки
Применение круглых скобок целесообразно, если под знаком тригонометрической функции находится отрицательное число или многочлен. Символы определяют принадлежность выражения к данной функции. Примеры: \[\operatorname{tg}(-3), \sin (x+5), \operatorname{tg}\left(\frac{1}{y}-5 \frac{1}{4}\right)\].
Нет смысла в применении ограничений, если под знаком тригонометрической функции присутствует выражение с корнем или степенью. Примеры: \[\sin \sqrt{x^{3}+1}, \operatorname{ctg} 2^{3}\].
Скобки не используют при наличии в выражении кратных углов. Например, \[\sin 2 \alpha, \operatorname{ctg} 5 x\]. Иногда они бывают нужны обязательно, чтобы избежать двусмысленности в записи. Например, \[\cos (3 \cdot x): 2, \text { a нe } \cos 3 \cdot x: 2\].
Примеры по математике со скобками в выражениях, содержащих логарифмы
Как правило, выражения, находящиеся под знаком логарифма, заключают в скобки.
Примеры: \[\lg \left(\mathrm{e}^{-2}-\mathrm{e}\right), \log _{s}-\left(x^{3}+2 x^{2}+1\right), \lg ((x-3) \cdot(x+5))\].
Пренебречь их использованием возможно, когда принадлежность выражения к логарифму понятна однозначно. Это касается дробей или корней: \[\log _{3} x^{4}, \lg \sqrt{x-3}, \ln \frac{5 \cdot x-4}{\sqrt{5}-1}\]
Скобки и выражения с пределами
Если выражение, относящееся к пределу, представлено в виде суммы, разности, частного или произведения, то его заключают в скобки.
Примеры:
Без обособления можно обойтись, если под знаком предела находится простая дробь или, как вариант, однозначно понятно, к какому выражению относится предел.
Пример: \[\lim _{x \rightarrow 1^{x}} \frac{3}{x}\].
Скобки и производные
Если под знаком производной находится сложное выражение, то следует воспользоваться круглыми скобками. Пример: \[(x+5)^{\prime},\left(\frac{\cos y}{y}-\sqrt{y-2}\right)^{\prime}\].
Запись подынтегральных выражений
Подынтегральные выражения записывают с использованием круглых скобок.
Примеры: \[\int\left(x^{3}+5 x\right) \mathrm{d} x, \int_{-1}^{1}(\cos 3 x-\sqrt{2}) \mathrm{d} x, \iiint(5 x y+2 z) \mathrm{d} x \mathrm{~d} y \mathrm{~d} z\].
Отделение аргумента функции скобками
Записывая функцию, как правило, пользуются круглыми скобками. Если функция обозначена литерой f, а аргумент — x, то общий вид функции — \[f(x)\]. При наличии нескольких аргументов функция имеет вид \[F(x, t, z)\].
Особенности написания периодических дробей
Скобки применяют при записи периодических дробей — в них заключают период. Например, если дробь имеет вид 0,54545454…, то ее можно записать в более компактном виде, характерном для периодических дробей: 0,(54). Еще один пример рациональной записи периодической дроби: 0,46(27). В обычном виде она выглядит следующим образом: 0,4627272727….

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Числовые промежутки
Существует несколько вариантов записи числовых промежутков при помощи различных сочетаний круглых и квадратных скобок: (), (], [), []. Внутри границ указывают промежутки, в которых функция имеет смысл. Круглый символ означает, что число не принадлежит области определения, квадратный — принадлежит. Если при записи числового промежутка фигурирует знак бесконечности, то пользуются круглыми скобками.
Примеры: \[(0,3),\left[\frac{1}{2}, 15\right),\left(-5 \frac{1}{3},-1 \frac{3}{4}\right),[4,800],(-\infty,-8],(-5,+\infty), (-\infty,+\infty)\].
Иногда вместо круглых ограничений можно встретить обратные квадратные. Например, выражения \[(0,3) \text { и }] 0,3[\] — идентичны. Смысл выражения остается прежним.
Запись числовых промежутков с помощью знаков различных видов сведена в таблицу.
| Наименование промежутка | Обозначение | Запись при помощи неравенства |
| Открытый интервал | \[(a ; b)\] | \[a<x<b\] |
| Отрезок (сегмент) | \[[a ; b]\] | \[a \leq x \leq b\] |
| Полусегмент | \[[a ; b)\] | \[a \leq x<b\] |
| Полусегмент | \[(a ; b]\] | \[a<x \leq b\] |
| Луч | \[(-\infty ; c]\] | \[x \leq c\] |
| Все числа координатной прямой | \[(-\infty ;+\infty)\] | \[x \in R\] |
| Пустое множество | \[\varnothing\] | \[x \in \emptyset, x \in \] {} |
Отображение систем и совокупностей уравнений
Системы уравнений, неравенств, а также системы, содержащие как уравнения, так и неравенства, используют с фигурной скобкой {, размещенной слева. Сами уравнения (неравенства) записывают в столбик.
Пример 1: \[\left\{\begin{array}{l}
x^{2}-3 y=5 \\
2 x+4 y=7
\end{array}\right.\]
Пример 2: \[\left\{\begin{array}{l}
2 x^{2}-y^{2} \geq 3 \\
4 x+2 y<4
\end{array}\right.\]
Система с уравнениями и неравенствами:
Значение фигурных скобок на языке множеств — пересечение. В сущности, решение системы уравнений — это их пересечение, общее для всех. Термин «совокупность» означает «объединение». Знаком совокупности является не фигурная скобка, а квадратная. Принцип записи совокупности неравенств, уравнений, неравенств с уравнениями — такой же, как и для систем. Только фигурный символ заменен квадратным.
Пример 1:
Пример 2:
Можно также встретить сочетание системы с совокупностью.
Применение фигурных скобок для отображения кусочных функций
При записи кусочных функций применяют фигурные скобки, которые определяют функцию формулы с указанием числовых промежутков.
Функция модуля: \[|z|=\left\{\begin{array}{l}
z, \text { при } \geq 0 \\
-z, \text { при } z<0
\end{array}\right.\]
Обозначение координат точки
С этой целью применяют круглые скобки, в которых записывают координаты точки на прямой, в двух- или трехмерной координатной система. Возможна также запись координат точки, расположенной в n-мерном пространстве.
Пример 1: \[B(4)\]. Это означает, что точка B имеет на прямой координату 4.
Пример 2: \[k(1,3,5)\]. Точка k имеет координаты 1, 3 и 5 соответственно по осям абсцисс, ординат и аппликат.
Пересечение элементов множества
Пересечение элементов множества — один из вариантов их описания. Элементы множества записывают через запятую, заключив внутрь фигурных скобок. Пример такой записи: C= {1, 5, 8}. Множество содержит 3 элемента: числа 1, 5 и 8.
Координаты вектора
Это понятие используют при рассмотрении векторов в некоторой координатной системе. Координаты вектора записывают в фигурных или круглых скобках поочередно. Примеры записи координат векторов в двухмерной системе: \[\vec{b}_{\{0,-4\}} \text { или } \vec{b}(0,-4)\]. Такая запись означает, что вектор имеет координаты по осям абсцисс и ординат 0 и -4 соответственно. Если вектор рассматривается в пространственной координатной системе, внутри скобок указывают три координаты.
Пример 1: \[\overrightarrow{B C}\left(0,-4, \frac{3}{5}\right)\].
В вузах принята иная запись векторов в системе координат: над буквенным обозначением вектора, как правило, не ставят черточку или стрелку. Координаты записывают внутри скобок по очереди, разделяя их запятыми.
Пример 2: \[a=\left(3,5,7, \frac{1}{2}, 9\right)\]. Так записывают вектор в пятимерной системе.
Есть и иная форма записи: в круглых скобках столбиком.
Запись матричных элементов
Скобки используют при написании матриц. Элементы последних заключают в парные круглые скобки. Иногда вместо круглых знаков пользуются квадратными. При этом матрицы имеют одинаковый смысл, получаются равнозначными.
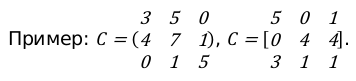
Надеемся, что приведенный материал окажется полезным при подготовке уроков математики.















